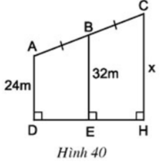
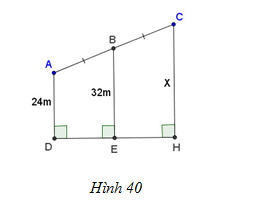
Tính x trên hình 40.
Những câu hỏi liên quan
Cho hình vuông ABCD, trên cạnh AB lấy điểm E , trên cạnh BC lấy điểm F sao cho AB = AE x 4 và BC = BF x 4. Tính tỉ số \(\frac{S_{DEF}}{S_{ABCD}}\)
Giúp mk với 
Sơ đồ minh họa:
Ta có:
\(S_{AED}=\frac{1}{2}\times AD\times AE=\frac{1}{2}\times AD\times\left(\frac{1}{4}\times AB\right)\)
\(=\frac{1}{8}\times AD\times AB=\frac{1}{8}\times S_{ABCD}\)
\(S_{BEF}=\frac{1}{2}\times BE\times BF=\frac{1}{2}\times\left(\frac{3}{4}\times AB\right)\times\left(\frac{1}{4}\times BC\right)\)
\(=\frac{3}{32}\times AB\times BC=\frac{3}{32}\times S_{ABCD}\)
\(S_{CDF}=\frac{1}{2}\times CD\times CF=\frac{1}{2}\times CD\times\left(\frac{3}{4}\times CB\right)\)
\(=\frac{3}{8}\times CD\times CB=\frac{3}{8}\times S_{ABCD}\)
Do đó: \(S_{AED}+S_{BEF}+S_{CDF}=\)
\(=\left(\frac{1}{8}+\frac{3}{32}+\frac{3}{8}\right)\times S_{ABCD}\)
\(=\frac{19}{32}\times S_{ABCD}\)
Suy ra:
\(S_{DEF}=S_{ABCD}-\left(S_{AED}+S_{BEF}+S_{CDF}\right)\)
\(=S_{ABCD}-\frac{19}{32}\times S_{ABCD}=\frac{13}{32}\times S_{ABCD}\)
Vậy \(\frac{S_{DEF}}{S_{ABCD}}=\frac{13}{32}\)
Đúng 0
Bình luận (0)
?5. Tính x trên hình 40.
Giúp mk nhá
Cảm ơn
Hình thang ACHD có :
BE // CH // AD
AB=BC
=> DE=EH
Xét hình thang ACHD có :
AB=BC
DE=EH
=> CE là đường trung bình của hình thang ACHD .
=> CE=(AD+CH):2
Mà AD=24 m ; CE=32 m
=> 32=(24+x):2
=> 24+x=32.2
=> 24+x=64
=> x=64-24
=> x=40
Vậy cạnh CH=40 m .
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
bài 58 : tìm số đo x trong hình 40 .hãy giải thích vì sao tính được như vậy ? 115 độ x? hình 40 ?
Đọc tiếp
bài 58 : tìm số đo x trong hình 40 .hãy giải thích vì sao tính được như vậy ? ?
Do trong hình có 2 đường thẳng cùng vuông góc với một đường thẳng nên 2 đt đó // với nhau
Do đó \(x+115^0=180^0\) (2 góc ở vị trí trong cùng phía)
Vậy \(x=180^0-115^0=65^0\)
Đúng 1
Bình luận (31)
vì 2 góc này cùng phía nên tổng bằng 180
có 180-115=65
Đúng 0
Bình luận (0)
Trên hình biết a // b và góc B2=40 độ:
a) Tính góc A1
b) So sánh góc A3 và B1
c) Tính góc A2+B1
Trên hình biết a // b và góc B2=40 độ:
a) Tính góc A1
b) So sánh góc A3 và B1
c) Tính góc A2+B1
\(a,a//b\Rightarrow\widehat{B_2}+\widehat{A_1}=180^0\left(trong.cùng.phía\right)\\ \Rightarrow\widehat{A_1}=180^0-40^0=140^0\\ b,a//b\Rightarrow\widehat{A_1}=\widehat{B_1}\left(đồng.vị\right)\\ Mà.\widehat{A_1}=\widehat{A_3}\left(đối.đỉnh\right)\\ \Rightarrow\widehat{A_3}=\widehat{B_1}\\ c,Ta.có.\widehat{A_2}+\widehat{B_1}=\widehat{A_2}+\widehat{A_1}=180^0\left(kề.bù\right)\)
Đúng 1
Bình luận (1)
a. Ta có: a // b
=> \(\widehat{B_2}+\widehat{A_1}=180^o\) (2 góc trong cùng phía)
Mà \(\widehat{B_2}=40^o\)
=> \(\widehat{A_1}=180^o-40^o=140^o\)
b. Ta có: \(\widehat{A_1}=\widehat{B_3}\) (so le trong) (1)
Ta lại có: \(\left\{{}\begin{matrix}\widehat{A_1}=\widehat{A_3}\left(ĐĐ\right)\\\widehat{B_1}=\widehat{B_3}\left(ĐĐ\right)\end{matrix}\right.\) (2)
Từ (1) và (2), suy ra:
\(\widehat{A_3}=\widehat{B_1}\)
c. Ta có: a // b
=> \(\widehat{A_1}=\widehat{B_1}=140^o\) (đồng vị)
\(\widehat{B_2}=\widehat{A_2}=40^o\) (đồng vị)
=> \(\widehat{A_2}+\widehat{B_1}=140^o+40^o=180^o\)
Đúng 0
Bình luận (0)
một hình chữ nhật ABCD có chu vi là 180 cm.
a) tính chiều dài hình chữ nhật ABCD? ( Biết chiều rộng của hình chữ nhật đó là 40 cm)
b) trên AB lấy điểm M sao cho AM bẳng chiều rộng của hình chữ nhật ABCD. Trên DC lấy điểm N sao AM = DN . Tính chu vi hình vuông AMND
Cho tam giác ABC vuông ở A, biết: AB = 30 cm, AC = 40 cm và BC =-x AC. Điểm D trên cạnh AB, điểm E trên cạnh AC sao cho hình thang BDEC có độ dài đường cao băng 9,6 cm và có hai đáy là DE và BC. a) Tính diện tích của hình tam giác ABC b) Tính diện tích của hình tam giác ADE
câu a mình chịu nhé
câu b: DIện tích tam giác ADE= 337,5 cm2
Trên một mảnh đất hình chữ nhật người ta dùng 40% diện tích để làm nhà thì còn lại 600 m2 .
A. Tính diện tích mảnh đất hình chữ nhật đó.
B. Tính chu vi mảnh đất ,biết chiều dài là 40 m.
Mình cần gấp!
# Giải:
a) 600 m2 đất ứng với số phần trăm là :
100% - 40% = 60%
Diện tích mảnh đất là :
600 : 60 . 100 = 1000 (m2)
b) Chiều rộng của mảnh đất là :
1000 : 40 = 25 (m)
Chu vi của mảnh đất là :
( 40 + 25 ) . 2 = 130 (m)
Vậy...
#By_Ami
Hai gen A và B cùng nằm trên một nhóm gen liên kết cách nhau 40 cm, hai gen C và D cùng nằm trên một NST với tần số hoán vị gen là 30%. Ở đời con của phép lai
A
b
a
B
C
D
a
d
x
a
b
a
b...
Đọc tiếp
Hai gen A và B cùng nằm trên một nhóm gen liên kết cách nhau 40 cm, hai gen C và D cùng nằm trên một NST với tần số hoán vị gen là 30%. Ở đời con của phép lai A b a B C D a d x a b a b C d c d , loại kiểu hình đồng hợp lặn về tất cả các tính trạng chiếm tỉ lệ:
A. 1,5%.
B. 1,75%.
C. 3,5%.
D. 7%.
