Rút gọn rồi tính giá trị của biểu thức sau tại x = -1/3.
Những câu hỏi liên quan
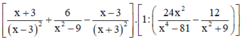
1 a. Rút gọn biểu thức sau A = \(\left(x^{\text{2}}-2x+4\right):\left(x^3+8\right)-x^2\) rồi tính giá trị của A tại x = -2
b. Rút gọn biểu thức B = (x - 2) : 2x + 5x rồi tính giá trị của biểu thức B tại x = 0
Rút gọn rồi tính giá trị các biểu thức sau: 4 x - 9 x 2 + 6 x + 1 t ạ i x = - 3
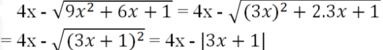
Tại x = -√3 ta được:
= 4(-√3) - |3(-√3) + 1|
= -4√3 - |-3√3 + 1|
= -4√3 - (3√3 - 1)
= -7√3 + 1
Đúng 0
Bình luận (0)
26 tháng 5 2022 lúc 22:13
Rút gọn rồi tính giá trị của biểu thức sau tại x =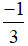 
.
Tham khảo:
* Rút gọn biểu thức:
+ Ngoặc thứ nhất:
+ Ngoặc thứ hai:
Do đó:
* Tại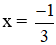 
, giá trị biểu thức bằng: 
Đúng 4
Bình luận (2)
10 tháng 12 2023 lúc 22:49
Rút gọn biểu thức sau rồi tính giá trị biểu thức
H = (x - 1)³ - (x + 2) (x² - 2x + 4) + 3(x + 4) (x - 4) tại x = 1/-2
Lời giải:
$H=(x^3-3x^2+3x-1)-(x^3+8)+3(x^2-16)$
$=x^3-3x^2+3x-1-x^3-8+3x^2-48$
$=(x^3-x^3)+(-3x^2+3x^2)+3x+(-1-8-48)$
$=3x-57=3.\frac{-1}{2}-57=\frac{-117}{2}$
Đúng 0
Bình luận (2)
1 . Rút gọn biểu thức B = (x - 2) : 2x + 5x rồi tính giá trị của biểu thức B tại x = 0
\(ĐK:x\ne0\)
Vậy tại x=0 thì k có gt nào của B thỏa mãn
Đúng 1
Bình luận (0)
Rút gọn biểu thức sau, rồi tìm giá trị của x để giá trị của biểu thức rút gọn là 1 số dương:
\(\dfrac{8-2x}{x^2+x-20}\)
\(\dfrac{8-2x}{x^2+x-20}=-\dfrac{2\left(4-x\right)}{\left(4-x\right)\left(x+5\right)}=\dfrac{-2}{x+5}\)
Để biểu thức trên nhận giá trị dương khi
\(x+5< 0\)do -2 < 0
\(\Leftrightarrow x< -5\)
Đúng 0
Bình luận (0)
Rút gọn rồi tính giá trị của biểu thức:(x-y)(x^2+xy+y^2)-2y^3 tại x=1/2 và y=2/3
Rút gọn rồi tính giá trị của biểu thức:\(\sqrt{\dfrac{\left(x-3\right)^2}{\left(3-x\right)^2}}+\dfrac{x^2-1}{x-3}\) (x<3) tại x= 0,5
Ta có: \(\sqrt{\dfrac{\left(x-3\right)^2}{\left(3-x\right)^2}}+\dfrac{x^2-1}{x-3}\)
\(=\dfrac{\left|x-3\right|}{\left|3-x\right|}+\dfrac{x^2-1}{x-3}\)
\(=\dfrac{3-x}{x-3}+\dfrac{x^2-1}{x-3}\)
\(=\dfrac{x^2-x+2}{x-3}\)
\(=\dfrac{-7}{10}\)
Đúng 0
Bình luận (0)
Rút gọn rồi tính giá trị các biểu thức sau: 1 - 10 a - 25 a 2 - 4 a t ạ i a = 2
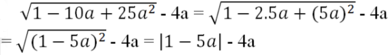
Tại a = √2 ta được:
= |1 - 5√2| - 4√2
= (5√2 - 1) - 4√2
= √2 - 1
Đúng 0
Bình luận (0)