Cho hình bình hành ABCD. Phép tịnh tiến T D A → biến:
A. B thành C
B. C thành A
C. C thành B
D. A thành D
Câu 1: Cho hình bình hành ABCD. Phép tịnh tiến \(T_{\overrightarrow{DA}}\) biến
A. B thành C
B. C thànhB
C. C thành A
D. A thành D
Câu 2: Cho hình bình hành ABEF. Gọi D,C lần lượt là trung điểm của AF và BF, O là giao điểm của AC và BD, I là giao điểm của FC và DE. Phép tịnh tiến \(T_{\overrightarrow{FI}}\) biến tam giác DIF thành tam giác nào sau đây:
A. \(\Delta AOD\)
B. \(\Delta CIE\)
C. \(\Delta OBC\)
D. \(\Delta OCI\)
Câu 3: Trong mặt phẳng, phép tịnh tiến \(T_{\overrightarrow{v}}\left(A\right)=B\) và \(T_{\overrightarrow{v}}\left(C\right)=D\) với \(\left(\overrightarrow{v}\ne\overrightarrow{0}\right)\) Mệnh đề nao sau đây sai?
A. \(\overrightarrow{AC}=\overrightarrow{BD}\)
B. \(\overrightarrow{AB}=\overrightarrow{CD}\)
C. \(\overrightarrow{AD}=\overrightarrow{CB}\)
D. \(AB=CD\)
Câu 4: Trong mặt phẳng tọa độ Oxy cho \(\overrightarrow{v}=\left(3;1\right)\). Tìm tọa độ của điểm \(M'\) là ảnh của điểm \(M\left(-2;1\right)\) qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}\)
A. \(M'\left(5;0\right)\)
B. \(M'\left(1;2\right)\)
C. \(M'\left(-5;0\right)\)
D. \(M'\left(5;2\right)\)
Câu 5: Trong mặt phẳng tọa độ Oxy cho điểm \(M\left(-2;1\right)\). Tìm tọa độ điểm N sao cho M là ảnh của N qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}=\left(-3;2\right)\)
A. N(1;3)
B. N(1;-1)
C. N(-1;-1)
D. N(-5;3)
Câu 6: Trong mặt phẳng tọa độ Oxy, cho hai điểm M(2;3) và N(1;-1). Phép tịnh tiến theo véc tơ \(\overrightarrow{v}\) biến điểm M thành điểm N. Khi đó ta có:
A.\(\overrightarrow{v}=\left(3;2\right)\)
B. \(\overrightarrow{v}=\left(-1;-4\right)\)
C. \(\overrightarrow{v}=\left(1;4\right)\)
D. \(\overrightarrow{v}=\left(-3;2\right)\)
Câu 7: Trong mặt phẳng Oxy và đường tròn \(\left(C\right):x^2+y^2-2x+4y-4=0\). Viết phương trình đường tròn (C') là ảnh của (C) qua \(T\overrightarrow{v}\)
A. \(\left(x-4\right)^2+\left(y-1\right)^2=4\)
B. \(\left(x+4\right)^2+\left(y+1\right)=9\)
C. \(\left(x-4\right)^2+\left(y-1\right)^2=9\)
D. \(x^2+y^2+8x+2y-4=0\)
Câu 8: Trong mặt phẳng tọa độ, xác định của đường thẳng \(\left(d\right):x+y-2=0\) qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}=\left(-3;0\right)\)
A. x+y+3=0
B. x-y-2=0
C. x+y+2=0
D. x+y+1=0
Cho hình bình hành ABCD. Phép tịnh tiến T A B → + A D → biến điểm A thành điểm:
A. A’ đối xứng với A qua C
B. A’ đối xứng với D qua C
C.O là giao điểm của AC và BD
D. C
Cho hình bình hành ABCD. Phép tịnh tiến T A B → + A D → biến điểm A thành điểm:
A. A’ đối xứng với A qua C
B. A’ đối xứng với D qua C
C.O là giao điểm của AC và BD
D. C
Số phát biểuđúng là:
a) Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó
b) Phép biến hình biến đường tròn thành đường tròn có bán kính bằng nó là phép tịnh tiến
c) Phép tịnh tiến biến tứ giác thành tứ giác bằng nó
d) Phép tịnh tiến biến đường tròn thành chính nó
e) Phép đồng nhất biến mọi hình thành chính nó
f) Phép dời hình là 1 phép biến hình không làm thay đồi khoảng cách giữa hai điểm bất kì
g) Phép chiếu lên đường thẳng không là phép dời hình
h) Với bất kì 2 điểm A, B và ảnh A’, B’ của chúng qua 1 phép dời hình, ta luôn có A’B = AB’.
i) Nếu phép dời hình F biến tam giác ABC thành tam giác A’B’C’ thì trọng tâm tam giác ABC biến thành trọng tâm tam giác A’B’C’.
k) Phép tịnh tiến theo vectơ là phép đồng nhất.
l) Nếu phép dời hình biến điểm A thành điểm B ( B ≠ A ) thì nó cũng biến điểm B thành A
m) Nếu phép dời hình biến điểm A thành điểm B và biến điểm B thành điểm C thì AB = BC
A.5
B.6
C.7
D.8
Đáp án D
Phát biểuđúng: a , c, e, f, g, i, j, l
b. Phép biến hình biến đường tròn thành đường tròn có bán kính bằng nó có thể là phép tịnh tiến
d. Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính
h. Với bất kì 2 điểm A, B và ảnh A’, B’ của chúng qua 1 phép dời hình, ta luôn có AB = A’B’.
k. Nếu phép dời hình biến điểm A thành điểm B thì nó cũng biến điểm B thành A (phát biểu không đúng với phép tịnh tiến)
Cho hai điểm phân biệt A, B và đường thẳng d. Hãy tìm một phép tịnh tiến, phép đối xứng trục, phép đối xứng tâm, phép quay, phép vị tự.
a. Biến A thành chính nó;
b. Biến A thành B;
c. Biến d thành chính nó.
a. Các phép biến một điểm A thành chính nó:
Phép đồng nhất:
- Phép tịnh tiến theo vectơ 0 .
- Phép quay tâm A, góc φ = 0º.
- Phép đối xứng tâm A.
- Phép vị tự tâm A, tỉ số k = 1.
- Ngoài ra còn có:
- Phép đối xứng trục mà trục đi qua A.
b. Các phép biến hình biến điểm A thành điểm B:
- Phép tịnh tiến theo vectơ AB .
- Phép đối xứng qua đường trung trực của đoạn thẳng AB.
- Phép đối xứng tâm qua trung điểm của AB.
- Phép quay mà tâm nằm trên đường trung trực của AB.
- Phép vị tự mà tâm là điểm chia trong hoặc chia ngoài đoạn thẳng AB theo tỉ số k.
c. Phép tịnh tiến theo vectơ v //d.
- Phép đối xứng trục là đường thẳng d’ ⊥ d.
- Phép đối xứng tâm là điểm A ∈ d.
- Phép quay tâm là điểm A ∈ d, góc quay φ =180º.
- Phép vị tự tâm là điểm I ∈ d.
Cho hình vuông ABCD có tâm I.
a.Xác định hình H1 là ảnh của hình vuông ABCD qua phép tịnh tiến theo vecto AI.
b. Xác định hình H2 là ảnh H1 qua phép tịnh tiến vecto IB.
c. Có 1 phép tịnh tiến nào biến H2 thành hình vuông ABCD.
Bài 1: Cho hình vuông ABCD tâm I. Gọi M,N lần lượt là trung điểm của AD, DC.Tìm phép tịnh tiến biến \(\Delta AMI\) thành \(\Delta MDN\).
Bài 2: Cho hình bình hành ABCD. Trình bày các phép tình tiến biến đường thẳng AB thành đường thẳng CD và biến đường thẳng AD thành đường thẳng BC.
Bài 3: Trong mặt phẳng tọa độ Oxy, cho \(\Delta ABC\) biết A(2;4), B(5;1), C(-1;-2). Phép tình tiến theo véctơ \(\overrightarrow{BC}\) biến \(\Delta ABC\) thành \(\Delta A'B'C'\) tương ứng các điểm. Tìm tọa độ trọng tâm G' của \(\Delta A'B'C'\).
Cho hai điểm phân biệt A, B và đường thẳng d. Hãy tìm một phép tịnh tiến, phép đối xứng trục, phép đối xứng tâm, phép quay, phép vị tự thỏa mãn một trong các tính chất sau :
a) Biến A thành chính nó
b) Biến A thành B
c) Biến d thành chính nó
a)
Các phép biến hình lần lượt là: Phép tịnh tiến theo véc tơ \(\overrightarrow{0}\); Phép quay tâm A góc \(\phi\) bất kì; phép vị tự tâm A tỉ số k bất kì.
b)
Phép tịnh tiến theo véc tơ \(\overrightarrow{AB}\); Phép đối xứng tâm qua trung điểm của AB; Phép quay tâm I là trung điểm của AB và góc \(\phi=90^o\); Phép vị tự tâm A tỉ số \(k=AB\).
c)
Phép tịnh tiến theo một véc tơ bất kì; Phép đối xứng tâm có tâm đối xứng nằm trên đường thẳng d; Phép quay bất kì; Phép vị tự có tâm nằm trên đường thẳng d.
Cho hai tam giác đều ABE và BCD bằng nhau trên hình 1.5. Tìm phép tịnh tiến biến ba điểm A, B, E theo thứ tự thành ba điểm B, C, D.
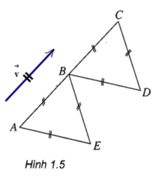
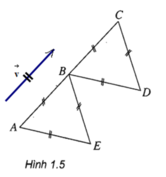
Phép tịnh tiến biến ba điểm A, B, E theo thứ tự thành ba điểm B, C, D là phép tịnh tiến theo v→ như hình vẽ trên: vecto v→=AB→
Trong mặt phẳng toạ độ Oxy, cho hình bình hành ABCD với A(1;-4), B(8;2) và giao điểm của 2 đường chéo AC và BD là I(3;-2).Nếu T là phép tịnh tiến theo vecto u biến đoạn thẳng AB thành đoạn thẳng CD thì vecto u có toạ độ là