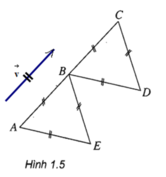
Phép tịnh tiến biến ba điểm A, B, E theo thứ tự thành ba điểm B, C, D là phép tịnh tiến theo v→ như hình vẽ trên: vecto v→=AB→

Phép tịnh tiến biến ba điểm A, B, E theo thứ tự thành ba điểm B, C, D là phép tịnh tiến theo v→ như hình vẽ trên: vecto v→=AB→
Số phát biểuđúng là:
a) Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó
b) Phép biến hình biến đường tròn thành đường tròn có bán kính bằng nó là phép tịnh tiến
c) Phép tịnh tiến biến tứ giác thành tứ giác bằng nó
d) Phép tịnh tiến biến đường tròn thành chính nó
e) Phép đồng nhất biến mọi hình thành chính nó
f) Phép dời hình là 1 phép biến hình không làm thay đồi khoảng cách giữa hai điểm bất kì
g) Phép chiếu lên đường thẳng không là phép dời hình
h) Với bất kì 2 điểm A, B và ảnh A’, B’ của chúng qua 1 phép dời hình, ta luôn có A’B = AB’.
i) Nếu phép dời hình F biến tam giác ABC thành tam giác A’B’C’ thì trọng tâm tam giác ABC biến thành trọng tâm tam giác A’B’C’.
k) Phép tịnh tiến theo vectơ là phép đồng nhất.
l) Nếu phép dời hình biến điểm A thành điểm B ( B ≠ A ) thì nó cũng biến điểm B thành A
m) Nếu phép dời hình biến điểm A thành điểm B và biến điểm B thành điểm C thì AB = BC
A.5
B.6
C.7
D.8
Cho hai điểm phân biệt A, B và đường thẳng d. Hãy tìm một phép tịnh tiến, phép đối xứng trục, phép đối xứng tâm, phép quay, phép vị tự.
a. Biến A thành chính nó;
b. Biến A thành B;
c. Biến d thành chính nó.
Cho ba điểm A, B, C thẳng hang theo thứ tự đó và AB = 2BC. Dựng các hình vuông ABEF, BCGH (đỉnh của hình vuông tính theo chiều kim đồng hồ). Xét phép quay tâm B góc quay - 90 0 biến điểm E thành điểm A. Gọi I là giao điểm của EC và GH. Giả sử I biến thành điểm J qua phép quay trên. Nếu AC = 3 thì IJ bằng bao nhiêu?
A . 2 10
B . 5
C . 2 5
D . 10
Cho tam giác ABC có G là trọng tâm. Dựng ảnh của tam giác ABC qua phép tịnh tiến theo vectơ AG . Dựng điểm D sao cho phép tịnh tiến theo vectơ AG biến D thành A.
Trong mặt phẳng tọa độ Oxy cho vectơ v → = - 1 ; 2 , A 3 ; 5 , B - 1 ; 1 và đường thẳng d có phương trình x – 2 y + 3 = 0 .
a. Tìm tọa độ của các điểm A' , B' theo thứ tự là ảnh của A, B qua phép tịnh tiến theo vecto v →
b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vectơ v →
c. Tìm phương trình của đường thẳng d' là ảnh của d qua phép tịnh tiến theo v .
Trong mặt phẳng tọa độ Oxy, cho các điểm A (1;1), B(0;3), C(2;4) .Xác định ảnh của tam giác ABC qua các phép biến hình sau.
(a)Phép tịnh tiến theo vector v = (2;1).
(b)Phép đối xứng qua trục Ox
(c)Phép đối xứng qua tâm I(2;1).
(d)Phép quay tâm O góc 90 o .
(e)Phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng qua trụ Oy và phép vị tự tâm O tỉ số k = -2
trong mp tọa độ xOy cho tam giác ABC với A(3;0) B(-2;4) C(-4;5) gọi G là trọng tâm tam giác ABC và phép tịnh tiến Tv biến A thành G. trong phép tịnh tiến nói trên G iến thành G' có tọa độ bằng bao nhiu? gọi H là rực tâm của tam giác ABC, tìm ảnh của H qua Tv?
Cho tam giác ABC. Gọi A’,B’,C’ lần lượt là trung điểm các cạnhBC, CA,AB. Phép tịnh tiến vectơ C B ' → biến DB’A’C thành :
A. △ B’C’A’
B. △ AC’B’
C. △ BC’A’
D. △ CA’B’
Số phát biểuđúng:
1. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với nó
2. Phép biến hình biến mỗiđiểm M thành chính nó dọi là phép đồng nhất
3. Phép đối xứng trục, phép quay, phép tịnh tiến đều bảo toàn khoảng cách giữa hai điểm
4. Phép đối xứng tâm biến đường thẳng thành đường thẳng song song với nó
5. Phép vị tự là một phép đồng dạng
6. Phép biến hình F’ có được nhờ thực hiện liên tiếp các phép tịnh tiến, phép quay, phép vị tự là phép đồng dạng
7. Phép biến hình F’ có được nhờ thực hiện liên tiếp các phép tịnh tiến, phép quay, phép vị tự là phép dời hình
A.4
B.5
C. 6
D.7