Cho số thực a ≠ 0 . Đặt b = ∫ − a a 1 2 a + x e x d x . Tính I = ∫ 0 2 a e x 3 a − x d x theo a và b
A. I = b e a
B. I = b e a
C. I = b . e a
D. I = a e b
Những câu hỏi liên quan
Cho số thực
a
≢
0
. Đặt
b
∫
-
a
a
1
2
a
+
x
e
x
d
x
. Tính
I
∫
0
2
a
e
x...
Đọc tiếp
Cho số thực a ≢ 0 . Đặt b = ∫ - a a 1 2 a + x e x d x . Tính I = ∫ 0 2 a e x 3 a - x theo a và b.
A. I = b e a
B. I = b e a
C. I = b . e a
D. I = a e b
Cho số thực
a
≠
0
. Đặt
b
∫
-
a
a
1
(
2
a
+
x
)
.
e
x
d
x
. Tính
I
...
Đọc tiếp
Cho số thực a ≠ 0 . Đặt b = ∫ - a a 1 ( 2 a + x ) . e x d x . Tính I = ∫ 0 2 a e x 3 a - x d x theo a và b.
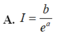
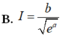
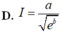
Cho số thực a thoả mãn (a-1)^3=9a. Đặt b= a^2+a. CMR (b+1)^3=27b^2
Cho các mệnh đề sau:(I). Nếu
a
b
c
t
h
ì
2
ln
a
ln
b
+
ln
c
(II). Cho số thực 0 a ≠ 1. Khi đó
a
-
1
log
a
x
≥
0...
Đọc tiếp
Cho các mệnh đề sau:
(I). Nếu a = b c t h ì 2 ln a = ln b + ln c
(II). Cho số thực 0 < a ≠ 1. Khi đó a - 1 log a x ≥ 0 ⇔ x ≥ 1
(III). Cho các số thực 0 < a ≠ 1 , b > 0 , c > 0 . Khi đó b log a c ≥ 0 ⇔ x ≥ 1
(IV). l i m x → + ∞ 1 2 x = - ∞ .
Số mệnh đề đúng trong các mệnh đề trên là
A. 3
B. 4
C. 2
D. 1
Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:
Đúng 0
Bình luận (0)
Xác định tính đúng sai của mỗi mệnh đề sau:
a) Nếu \(2a - 1 > 0\) thì \(a > 0\) (a là số thực cho trước).
b) \(a - 2 > b\) nếu và chỉ nếu \(a > b + 2\) (a, b là hai số thực cho trước).
a) Mệnh đề có dạng \(P \Rightarrow Q\) với P: “\(2a - 1 > 0\)” và Q: “\(a > 0\)”
Ta thấy khi P đúng (tức là \(a > \frac{1}{2}\)) thì Q cũng đúng. Do đó, \(P \Rightarrow Q\) đúng.
b) Mệnh đề có dạng \(P \Leftrightarrow Q\) với P: “\(a - 2 > b\)” và Q: “\(a > b + 2\)”
Khi P đúng thì Q cũng đúng, do đó, \(P \Rightarrow Q\) đúng.
Khi Q đúng thì P cũng đúng, do đó, \(Q \Rightarrow P\) đúng.
Vậy mệnh đề \(P \Leftrightarrow Q\) đúng.
Đúng 0
Bình luận (0)
Cho hai số thực dương a, b với a khác 1. Đặt
M
log
a
b
. Tính M theo
N
log
a
b
. A.
M
N
B. M 2N C.
M
1
2
N
D.
M
N
2
Đọc tiếp
Cho hai số thực dương a, b với a khác 1. Đặt M = log a b . Tính M theo N = log a b .
A. M = N
B. M = 2N
C. M = 1 2 N
D. M = N 2
Cho số phức
z
a
+
b
i
(
a
,
b
∈
R
)
. Xét các mệnh đề sau :(1) z là số thực khi và chỉ khi
a
≠
0
,
b
0
(2) z là số thuần ảo khi và chỉ khi
a
0
,
b
≠
0
(3) z vừa là số thực vừa là số thuần ảo khi và chỉ khi a 0, b 0Số mệ...
Đọc tiếp
Cho số phức z = a + b i ( a , b ∈ R ) . Xét các mệnh đề sau :
(1) z là số thực khi và chỉ khi a ≠ 0 , b = 0
(2) z là số thuần ảo khi và chỉ khi a = 0 , b ≠ 0
(3) z vừa là số thực vừa là số thuần ảo khi và chỉ khi a = 0, b = 0
Số mệnh đề đúng là ?
A. 2
B. 0
C. 3
D. 1
Cho hai số thực a, b với
a
0
,
a
≠
1
,
b
≠
0
. Khẳng định nào sau đây sai? A.
log
a
3
b
1
2
log
a
b
B.
1
2
log
a...
Đọc tiếp
Cho hai số thực a, b với a > 0 , a ≠ 1 , b ≠ 0 . Khẳng định nào sau đây sai?
A. log a 3 b = 1 2 log a b
B. 1 2 log a b 2 = log a b
C. 1 2 log a a 2 = 1
D. 1 2 log a b 2 = log a b
Chọn D.
Phương pháp
Xét tính đúng sai của từng đáp án, chú ý các tính chất của logarit.
Cách giải:
Dễ thấy các đáp án A, B, C đều đúng theo tính chất logarit. Đáp án D sai vì chưa biết b > 0 hay b < 0 nên
không phá được dấu giá trị tuyệt đối trong đáp án D.
Đúng 0
Bình luận (0)
Cho a, b là các số thực dương và a khác 1, đặt
P
log
a
2
b
6
+
2
log
a
b
4
. Mệnh đề nào dưới đây đúng? A.
P
10
log
a
b
B.
P
19...
Đọc tiếp
Cho a, b là các số thực dương và a khác 1, đặt P = log a 2 b 6 + 2 log a b 4 . Mệnh đề nào dưới đây đúng?
A. P = 10 log a b
B. P = 19 log a b
C. P = 7 log a b
D. P = 16 log a b
