Cho tứ giác ABCD. Gọi E, F theo thứ tự là trung điểm của AB và CD; M, N, P, Q lầ lượt là trung điểm của các đoạn thẳng AF, CE, BF và DE. Gọi I là giao điểm của MP và EF. Chứng minh rằng:
a) I là trung điểm của MP
b) MNPQ là hình bình hành
cho tứ giác ABCD có AD=BC. gọi H,K theo thứ tự là trung điểm của AB và CD. GỌI E,F theo thứ tự là giao điểm của đường thẳng AD,BC với đường thẳng HK.Chứng minh rằng góc E= góc F
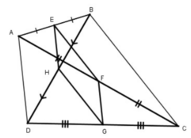
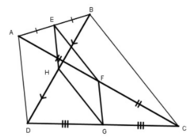
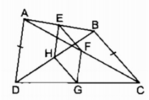
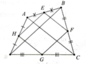
cho điểm O nằm trong tứ giác ABCD . E,F,G,H theo thứ tự là trung điểm của AB,BC,CD,DA . Gọi M,N,P,Q theo thứ tự là các điểm đối xứng với O qua E,F,G,H
CM : MNPQ là hbh và có các cạnh = đường chéo của tứ giác ABCD
Em tự vẽ hình nhé. Ý sau cô nói rõ yêu cầu hơn là chứng minh hình bình hành MNPQ có chu vi bằng tổng độ dài hai đường chéo của tứ giác ABCD.
Xét tứ giác EFMN có OF = ON; OE = OM nên nó là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Vậy thì MN // EF // AC và MN = EF = AC / 2 (Vì EF là đường trung bình tam giác BAC).
Hoàn toàn tương tự: QP // GH // AC và QP = GH = AC/2.
Vậy MNPQ là hình bình hành (Cặp cạnh đối song song và bằng nhau).
Khi đó ta có:
\(p_{MNPQ}=PQ+PN+NM+MQ=\left(PQ+MN\right)+\left(MQ+PN\right)=AC+BD.\)
Vậy ta đã chứng minh xong bài toán.
Cô ơi em ko hiểu.Theo em thì ta phải cm MN//=AC và PQ//=AC
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, AC, CD, DB. Tìm điều kiện của tứ giác ABCD để EFGH là: Hình vuông
Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF là đường trung bình của tam giác ABC
Nên EF // BC, EF = 1/2 BC.
Xét tam giác BDC có
HB = HD, GD = GC (gt)
Nên HG là đường trung bình của tam giác BDC
Nên HG // BC, HG = 1/2 BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
EFGH là hình vuông khi và chỉ khi EFGH là hình chữ nhật đồng thời là hình thoi
⇔ AD ⊥ BC và AD = BC
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, AC, CD, DB. Tìm điều kiện của tứ giác ABCD để EFGH là: Hình thoi
Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF là đường trung bình của tam giác ABC
Nên EF // BC, EF = 1/2 BC.
Xét tam giác BDC có
HB = HD, GD = GC (gt)
Nên HG là đường trung bình của tam giác BDC
Nên HG // BC, HG = 1/2 BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
EFGH là hình thoi ⇔ EH = EF ⇔ AD = BC
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, AC, CD, DB. Tìm điều kiện của tứ giác ABCD để EFGH là: Hình chữ nhật
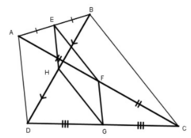
Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF là đường trung bình của tam giác ABC
Nên EF // BC, EF = 1/2 BC.
Xét tam giác BDC có
HB = HD, GD = GC (gt)
Nên HG là đường trung bình của tam giác BDC
Nên HG // BC, HG = 1/2 BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
EFGH là hình chữ nhật ⇔ EH ⊥ EF ⇔ AD ⊥ BC
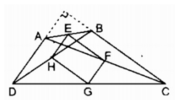
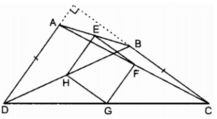
Cho hình bình hành ABCD có AB=2AD. Gọi E và F theo thứ tự là trung điểm của AB và CD. Các tứ giác AEFD, AECF là hình gì? Vì sao?
* Xét tứ giác AEFD, ta có:
AB // CD (gt) hay AE // FD
AE = 1/2 AB (gt)
FD = 1/2 CD (gt)
Suy ra: AE = FD
Tứ giác AEFD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
AD = AE = 1/2 AB . Vậy tứ giác AEFD là hình thoi.
* Xét tứ giác AECF, ta có: AE // CF (gt)
AE = 1/2 AB (gt)
CF = 1/2 CD (gt)
Suy ra: AE = CF
Tứ giác AECF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để tứ giác EFGH là hình chữ nhật ?
Chứng minh EFGH là hình bình hành. Để EFGH là hình chữ nhật thì
Þ H E F ^ = 90 0 ⇒ H E ⊥ E F
Þ AC ^BD.
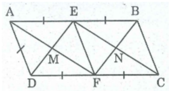
Cho hình bình hành ABCD có E, F theo thứ tự là trung điểm của AB, CD. Gọi giao điểm của AC với DE và BF theo thứ tự là M và N. Chứng minh rằng tứ giác EMFN là hình bình hành.
Xét ∆ EOM và ∆ FON có: ∠ (MEO) = ∠ (NFO) (so le trong do DE//BF)
OE = OF (tính chất hình bình hành)
∠ (MOE)= ∠ (NOF) (đối đỉnh )
Suy ra: ∆ EOM = ∆ FON (g.c.g) ⇒ OM = ON
Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).
Bài 1: Cho điểm O nằm trong tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Gọi M, N, P, Q theo thứ tự là các điểm đối xứng với O qua E, qua F, qua G, qua H. CMR: MNPQ là hình bình hành và có các cạnh bằng các đường chéo của tứ giác ABCD.
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, AC, CD và BD.
a) Chứng minh rằng tứ giác EFGH là hình bình hành.
b) Tìm điều kiện của tứ giác ABCD để EFGH là hình chữ nhật.
a: Xét ΔBAD có
E là tđiểm của AB
H là tđiểm của BD
Do đó: EH là đường trung bình của ΔABD
Suy ra: EH//AD và EH=AD/2(1)
Xét ΔACD có
F là trung điểm của AC
G là trung điểm của CD
Do đó: FG là đường trung bình của ΔACD
Suy ra: FG//AD và FG=AD/2(2)
Từ (1) và (2) suy ra EH//GF và EH=GF
hay EFGH là hình bình hành