Chứng minh phân thức - n + 3 n - 4 (với n ∈ N) là tối giản:

Những câu hỏi liên quan
Chứng minh phân thức \(\dfrac{3-n}{n-4}\) là tối giản:
Gọi d=ƯCLN(-n+3,n-4)
\(\Rightarrow-n+3⋮d;n-4⋮d\\ \Rightarrow-n+3+n-4⋮d\\ \Rightarrow-1⋮d\\ \Rightarrow d=1\\ \RightarrowƯCLN\left(-n+3,n-4\right)=1\)
Vậy ...
Đúng 2
Bình luận (0)
Chứng minh phân thức 2 n + 1 5 n + 3 (với n ∈ N) là tối giản
Hướng dẫn giải:
Gọi ƯCLN của 2n + 1 và 5n + 3 là d
⇒ (2n +1)⋮ d và (5n + 3)⋮ d
⇒ [2(5n + 3) - 5(2n + 1) ] ⋮ d
⇒ 1 ⋮ d, với ∀n ∈ N
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Đúng 0
Bình luận (0)
Chứng minh phân thức 3 n + 1 5 n + 2 (với n ∈ N) là tối giản
Hướng dẫn giải:
Gọi ƯCLN của 2n + 1 và 5n + 3 là d
⇒ (3n + 1) ⋮ d và (5n + 2) ⋮ d
⇒ [3(5n + 2) - 5(3n + 1)] ⋮ d
⇒ 1 ⋮ d, với ∀n ∈ N
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Đúng 1
Bình luận (0)
Cho phân thức m n là phân thức tối giản. Chứng minh phân thức m m + n là phân thức tối giản
Hướng dẫn giải:
Giả sử m, n là các số nguyên và ƯCLN(m, n) = 1 (vì 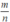 tối giản)
tối giản)
nếu d là ước chung m của m + n thì:
(m + n) d và m d
⇒ [(m + n) – m ] = n d
⇒ d ∈ ƯC (m,n) ⇒ d = 1(vì 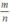 tối giản) .
tối giản) .
Vậy nếu phân thức 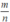 là phân thức tối giản thì phân thức
là phân thức tối giản thì phân thức 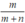 cũng là phân thức tối giản.
cũng là phân thức tối giản.
Đúng 0
Bình luận (0)
Chứng minh phân thức 3 n - 2 4 n - 3 là tối giản với mọi số tự nhiên n
Hướng dẫn giải:
Gọi d là ƯCLN của 3n - 2 và 4n - 3
⇒ (3n - 2)⋮ d và (4n - 3)⋮ d
⇒ [3(4n - 3) - 4(3n - 2)] = -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Đúng 0
Bình luận (0)
Chứng minh phân thức 3 n - 2 4 n - 3 là tối giản với mọi số tự nhiên n
Hướng dẫn giải:
Gọi d là ƯCLN của 3n - 2 và 4n - 3
⇒ (3n - 2)⋮ d và (4n - 3)⋮ d
⇒ [3(4n - 3) - 4(3n - 2)] = -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Đúng 0
Bình luận (0)
Chứng minh A= 3-n/n-4 ( n thuộc N , n khác 4) là phân số tối giản
Gọi d là UCLN(3-n;n-4)
\(\Leftrightarrow\left\{{}\begin{matrix}n-3⋮d\\n-4⋮d\end{matrix}\right.\Leftrightarrow1⋮d\)
=>UCLN(3-n;n-4)=1
=>A là phân số tối giản
Đúng 0
Bình luận (0)
a) Chứng minh rằng với mọi số tự nhiên n thì phân số 21n+4/14n+3 là phân số tối giản
b) Tìm tất cả các số tự nhiên n để phân số n+3/n-12 là phân số tối giản
c) Tìm các số tự nhiên n để phân số 21n+3/6n+4 rút gọn được
a) Để 21n+4/14n+3 là phân số tổi giản thì ƯCLN(21n+4; 14n+3) =1
Gọi ƯCLN(21n+4; 14n+3) =d => 21n+4 \(⋮\)d; 14n+3 \(⋮\)d
=> (14n+3) -(21n+4) \(⋮\)d
=> 3(14n+3) -2(21n+4) \(⋮\)d
=> 42n+9 - 42n -8 \(⋮\)d
=> 1\(⋮\)d
=> 21n+4/14n+3 là phân số tối giản
Vậy...
c) Gọi ƯC(21n+3; 6n+4) =d; 21n+3/6n+4 =A => 21n+3 \(⋮\)d; 6n+4 \(⋮\)d
=> (6n+4) - (21n+3) \(⋮\)d
=> 7(6n+4) - 2(21n+3) \(⋮\)d
=> 42n +28 - 42n -6\(⋮\)d
=> 22 \(⋮\)cho số nguyên tố d
d \(\in\){11;2}
Nếu phân số A rút gọn được cho số nguyên tố d thì d=2 hoặc d=11
Nếu A có thể rút gọn cho 2 thì 6n+4 luôn luôn chia hết cho 2. 21n+3 chia hết cho 2 nếu n là số lẻ
Nếu A có thể rút gọn cho 11 thì 21n+3 \(⋮\)11 => 22n -n +3\(⋮\)11 => n-3 \(⋮\)11 Đảo lại với n=11k+3 thì 21n+3 và 6n+4 chia hết cho 11
Vậy với n là lẻ hoặc n là chẵn mà n=11k+3 thì phân số đó rút gọn được
a) Cho biểu thức A=3/2+n n khác -2 Tìm các số nguyên n để A là một số nguyên.
b) Chứng minh phân số n+6/n=7 là phân số tối giản với mọi số n nguyên và n khác -7 .
a: Để A nguyên thì \(n+2\in\left\{1;-1;3;-3\right\}\)
=>\(n\in\left\{-1;-3;1;-5\right\}\)
b: n+6/n+7
Gọi d=ƯCLN(n+6;n+7)
=>n+6-n-7 chiahết cho d
=>-1 chia hết cho d
=>d=1
=>PSTG
Đúng 3
Bình luận (0)












