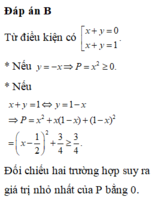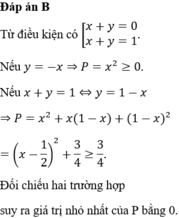\(A=x^2+y^2+z^2-yz-4x-3y+2027\)

\(\Rightarrow4A=4x^2+4y^2+4z^2-4yz-16x-12y+8108=4x^2-16x+16+3y^2+12y+12+y^2-4yz+4z^2+8080=4\left(x-2\right)^2+3\left(y+2\right)^2+\left(y-2z\right)^2+8080\)

Vì \(4\left(x-2\right)^2\ge0\)

    \(3\left(y+2\right)^2\ge0\)

     \(\left(y-2z\right)^2\ge0\)

\(\Rightarrow4A\ge8080\Rightarrow A\ge2020\)

\(ĐTXR\Leftrightarrow x=2,y=-2,z=-1\)

Bài 1: 

\(A=x^2+6x+9+x^2-10x+25\)

\(=2x^2+4x+34\)

\(=2\left(x^2+2x+17\right)\)

\(=2\left(x+1\right)^2+32>=32\forall x\)

Dấu '=' xảy ra khi x=-1

Ta có:  2 x 2 + 1 2 ≥ 2 x ;  2 y 2 + 1 2 ≥ 2 y và  x 2 + y 2 ≥ 2 x y

Cộng vế với vế các BĐT trên ta được:

3 x 2 + y 2 + 1 ≥ 2 x + y + x y = 5 2

=> A =  x 2 + y 2 ≥ 1 2

Từ đó tìm được  A m i n = 1 2 <=> x = y =  1 2

\(a,=3\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{4}=3\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\)

Dấu \("="\Leftrightarrow x=\dfrac{1}{2}\)

\(b,=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\)

Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)

\(c,=\left(x^2-2xy+y^2\right)+x^2+1=\left(x-y\right)^2+x^2+1\ge1\)

Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=y\\x=0\end{matrix}\right.\Leftrightarrow x=y=0\)

a) Từ M = x − 3 2 2 + 31 4 ≥ 31 4 ⇒ M min = 31 4 ⇔ x = 3 2 .  

b) Ta có N = ( x   +   2 y ) 2   +   ( y   –   2 ) 2   +   ( x   +   4 ) 2   –   120   ≥   -   120 .

Tìm được N min  = -120 Û x = -4 và y = 2.

Đặt A=\(\left|2x-3y\right|+\left|4z-3x\right|+\left|xy+yz+xz-2484\right|\)

Ta có \(\left|2x-3y\right|\ge0;\left|4z-3x\right|\ge0;\left|xy+yz+xy-2484\right|\ge0\)

\(\Rightarrow A\ge0\Rightarrow Amin=0\)

\(\Leftrightarrow\hept{\begin{cases}2x-3y=0\\4z-3x=0\\xy+yz+xz-2484=0\end{cases}\Leftrightarrow\hept{\begin{cases}\frac{x}{3}=\frac{y}{2}\Rightarrow\frac{x}{12}=\frac{y}{8}\left(1\right)\\\frac{x}{4}=\frac{z}{3}\Rightarrow\frac{x}{12}=\frac{z}{9}\left(2\right)\\xy+yz+xz=2484\left(3\right)\end{cases}}}\)

Từ (1)(2)\(\Rightarrow\frac{x}{12}=\frac{y}{8}=\frac{z}{9}=k\left(k\ne0\right)\)

\(\Rightarrow x=12k;y=8k;z=9k\)

Thay vào 3 ta có \(12.8.k^2+8.9.k^2+12.9.k^2=2484\)

\(\Rightarrow k^2\left(12.8+8.9+12.9\right)=2484\)

\(\Rightarrow k^2.276=2484\)

\(\Rightarrow k^2=9=\left(\pm3\right)^2\)

\(\Rightarrow k=\pm3\)

+Nếu k =3 thì      x=36          ;                  y=24                        ;                      z=27

+Nếu k = -3thì    x=-36          ;                   y=-24                      ;                        z=-27

Vậy \(Amin=0\Leftrightarrow\left(x;y;z\right)\in\left\{\left(36;24;27\right);\left(-36;-24;-27\right)\right\}\)