Cho ABC vuông ở A. Kẻ AH vuông góc với BC tại H. Kẻ HD vuông góc với AC tại D .
a) Chứng minh AB//HD
b)Tính góc AHD nếu biết góc B = 60o.
c)Tia phân giác góc BAH cắt tia phân giác góc ACB tại I .. CMR: \(AI\perp CI\)
Cho tam giác ABC vuông ở A. Kẻ AH vuông góc với BC tại H. Kẻ HD vuông góc với AC tại D.
a) Chứng minh AB//HD.
b) Tính góc AHD nếu biết góc B=60 độ.
b) Tia phân giác góc BAH cắt tia phân giác góc CAB tại I. Chứng minh rằng AI vuông góc với CI
a) AB// HD (cùng vuông góc với AC)
b) AB// HD suy ra ABC= DHC= 60 độ nên AHD= 30 độ ( vì kề bù với góc DHC= 60 độ và góc BAH= 90 độ)
c) bạn ghi sai đề phải là cắt tia phân giác góc BCA tại I
Ta có: BAC= 30 độ (trong tam giác HDC có DHC= 60 độ; HDC= 90 độ)
suy ra 1/2 BAC= 15 độ hay ACI= 15 độ
Cm tương tự với tam giác ABH ta đc BAH= 30 độ suy ra HAI= 15 độ
Cm tương tự vói tam giác HAD ta đc HAD= 60 độ
Xét tam giác IAC có IAC+ (IAH+HAC) + AIC= 180 độ
hay 15 độ+ 75 độ + AIC=180 độ
suy ra AIC= 90 độ hay AI vuông góc Ci
Cho tam giac ABC vuông tại A có AB = 6cm, AC = 8cm. Kẻ đường cao AH sao cho AH vuông góc với BC (H thuộc BC) a. Tính độ dài BC b. Tia phân giác góc HAC cắt cạnh BC tại D. Qua D kẻ DK vuông góc AC (K thuộc AC). Chứng minh tam giác AHD = AKD c. Chứng minh tam giác BAD cân d. Tia phân giác góc BAH cắt canh BC tại E. Chứng minh: AB + AC = BC + DE
câu d ai giúp vớiCho tam giác ABC vuông tại A . Tia phân giác góc B cắt AC tại D , tia phân giác góc C cắt AB tại E kẻ DH vuông góc với BC tại H, kẻ EK vuông góc với BC tại K a) Chứng minh BA=BH b) BD vuông góc với AH c) Chứng minh AB+AC=BC+HK d) Tính góc HAK
a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔBAD=ΔBHD
Suy ra: BA=BH
b: Ta có: ΔBAD=ΔBHD
nên DA=DH
hay D nằm trên đường trung trực của AH(1)
Ta có: BA=BH
nên B nằm trên đường trung trực của AH(2)
Từ (1) và (2) suy ra BD là đường trung trực của AH
hay BD⊥AH
Mình chỉ làm câu c, d thôi nha ( vì câu a, b bạn Nguyễn Lê Phước Thịnh làm rồi)
c) Xét tam giác ECK và tam giác ECA có:
EKC=EAC=90
EC cạnh chung
ECK=ECA ( vì CE là p/g của ABC)
=>Tam giác ECK=Tam giác ECA ( ch-gn)
=>CK=CA( 2 cạnh tương ứng)
Mà AB=HB( chứng minh a)
=>CK+BH=CA+AB
=>CH+KH+BK+HK=AC+AB
=>(BK+KH+CH)+HK=AC+AB
=>BC+HK=AB+AC (ĐPCM)
d) Ta có: \(\left\{{}\begin{matrix}CK=CA\left(theo.c\right)\\BA=BH\left(theo.a\right)\end{matrix}\right.\)=>Tam giác ACK cân tại C và tam giác ABH cân tại B
=>\(\left\{{}\begin{matrix}CAK=CKA=\dfrac{180-ACB}{2}\\BAH=BHA=\dfrac{180-ABC}{2}\end{matrix}\right.\)
Có: BAH+CAK=BAK+HAK+HAC+HAK=BAK+2HAK+HAC=\(\dfrac{180-ABC}{2}+\dfrac{180-ACB}{2}\)=\(\dfrac{360-\left(ABC+ACB\right)}{2}\)
=\(\dfrac{360-90}{2}=135\)
=>BAK+2HAK+HAC=135
Mà BAK+HAC=BAC-HAK=90-HAK
=>90-HAK+2HAK=135
=>90+HAK=135
=>HAK=45
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H , kẻ tia phân giác của góc BAH cắt BC tại D
a) So sánh góc BAH và góc C ; góc CAH và góc B ; góc DAC và góc ADC
b) Kẻ tia phân giác của góc ACB cắt AD tại K . Chứng minh CK vuông góc với AD
HELP ME !!!!!!!!!!
a) \(\widehat{BAH}=\widehat{C}\) (vì cùng phụ với \(\widehat{B}\)) (1)
\(\widehat{CAH}=\widehat{B}\) (vì cùng phụ với \(\widehat{C}\)) (2)
Xét tam giác DAB có: \(\widehat{ADC}=\widehat{DAB}+\widehat{B}\) (vì góc ngoài bằng tổng hai góc trong không kề với nó)
Ta lại có: \(\widehat{DAC}=\widehat{DAH}+\widehat{HAC}\)
Mà \(\widehat{DAB}=\widehat{DAH}\) (tính chất tia phân giác)
\(\widehat{B}=\widehat{HAC}\) (theo (2))
=> \(\widehat{ADC}=\widehat{DAC}\)
b) Theo câu a ta có: \(\widehat{C}=\widehat{HAB}\)
=> \(\widehat{C_1}=\widehat{C_2}=\widehat{A_1}=\widehat{A_2}\)
Xét tam giác ACK có tổng 2 góc A và C là:
\(\widehat{ACK}+\widehat{CAK}=\widehat{C_2}+\widehat{CAK}=\widehat{A_1}+\widehat{CAK}=\widehat{CAB}=90^o\)
=> Góc còn lại bằng 90 độ, tức là \(\widehat{AKC}=180^o-\left(\widehat{ACK}+\widehat{CAK}\right)=180^o-90^o=90^o\)
=> CK vuông góc với AD
Cho tam giác ABC vuông tại A, có AB < AC. Kẻ AH vuông góc với BC (H thuộc BC).
a) Chứng minh: HB < AH < HC.
b) Tia phân giác góc BAH cắt BC tại D. Qua C kẻ đường thẳng vuông góc với AD và cắt AD tại I.
Chứng minh: CI là tia phân giác của góc ACB.
c) Tia phân giác góc ADC cắt CI tại K, từ K vẽ KE vuông góc với BC (K thuộc BC).
Chứng minh: ID + IC > KE+ DC.
Cho tam giác ABC vuông tại A, có AB < AC. Kẻ AH vuông góc với BC (H thuộc BC).
a) Chứng minh: HB < AH < HC.
b) Tia phân giác góc BAH cắt BC tại D. Qua C kẻ đường thẳng vuông góc với AD và cắt AD tại I.
Chứng minh: CI là tia phân giác của góc ACB.
c) Tia phân giác góc ADC cắt CI tại K, từ K vẽ KE vuông góc với BC (K thuộc BC).
Chứng minh: ID + IC > KE+ DC.
Câu hỏi tương tự Đọc thêmToán lớp 7Hình họcggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggg
Cho tam giác ABC vuông tại A, có AB < AC. Kẻ AH vuông góc với BC (H thuộc BC).
a) Chứng minh: HB < AH < HC.
b) Tia phân giác góc BAH cắt BC tại D. Qua C kẻ đường thẳng vuông góc với AD và cắt AD tại I.
Chứng minh: CI là tia phân giác của góc ACB.
c) Tia phân giác góc ADC cắt CI tại K, từ K vẽ KE vuông góc với BC (K thuộc BC).
Chứng minh: ID + IC > KE+ DC.
cho tam giác ABC cân tại A . kẻ AH là tia phân giác của góc A. H thuộc BC . từ H kẻ HD vuông góc với AB , kẻ HE vuông góc với AC chứng minh ràng
a, tam giác AHD = tam giác AHE
B, Cho AB =10cm AH= 8CM Tính HC
c, AH vuông góc DE
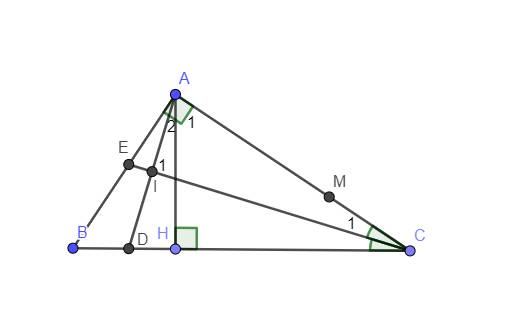
Cho tam giác ABC có góc A = 90 độ. Kẻ AH vuông góc với BC (H thuộc BC)
a) Chứng minh góc BAH = góc ACB.
b) Tia phân giác góc BAH và tia phân giác góc ACB cắt nhau tại I. Tính góc AIC
c) Cho AC > AB Trên cạnh AC lấy điểm M sao cho CM= AB. So sánh CM và BH.
`a)`
`Delta HAC` vuông tại `H` có :`hat(A_1)+hat(ACB)=90^0`
`hat(HAB)+hat(A_1)=90^0(kề bù)`
nên `hat(ACB)=hat(A_1)(đpcm)`
`b)`
`Delta HAC` vuông tại `H` có : `hat(A_1)+hat(ACH)=90^0`
hay `hat(A_1)+hat(ACB)=90^0`
`Delta ABC` vuông tại `A` có : `hat(B)=hat(ACB)=90^0`
nên `hat(B)=hat(A_1)`
Có `hat(IAC)=hat(A_1)+hat(A_2)`
`=1/2 hat(BAH)+hat(B)=1/2 hat(BCA) +hat(BAH)` (1)
`hat(C_1)=1/2 hat(ACB)(CI` là p/g của `hat(ACB)` `)`(2)
Từ `(1)` và `(2)=>hat(IAC)+hat(C_1)=hat(ABH)+hat(ACB)`
mà `hat(ABH)+hat(ACB)=90^0`
nên `hat(IAC)+hat(C_1)=90^0`
hay `hat(I_1)=90^0`
Cho tam giác ABC vuông tại A . Tia phân giác góc B cắt AC tại D , tia phân giác góc C cắt AB tại E kẻ DH vuông góc với BC tại H, kẻ EK vuông góc với BC tại K
a) Chứng minh BA=BH
b)BD vuông góc với AH
c)Chứng minh AB+AC=BC+HK
d)tính góc HAK