Tìm m để 3 đường thẳng sau đồng quy:
y = 2x - 1
y = (2m + 3)x - m + 1
y = x + 2

Những câu hỏi liên quan
Tìm m để 2 đường thẳng:
y = (m^2 - 6)x + 2m - 1
y = -2x + m - 3
a. Song song
b. Trùng nhau
Hai đường thẳng song song khi:
\(\left\{{}\begin{matrix}m^2-6=-2\\2m-1\ne m-3\end{matrix}\right.\) \(\Rightarrow m=2\)
Hai đường thẳng trùng nhau khi:
\(\left\{{}\begin{matrix}m^2-6=-2\\2m-1=m-3\end{matrix}\right.\) \(\Rightarrow m=-2\)
Đúng 1
Bình luận (0)
Tìm m để 2 đường thẳng
y = (3m + 2)x + m^2 - 1
y = (2m - 1)x + 8
cắt nhau tại 1 điểm trên trục tung
Giải thích các bước giải: pt hoành độ giao điểm 2x + m=x-2m+3(*)
để đường thẳng y = 2x + m và y = x-2m+3 cắt nhau tại 1 điểm nằm trên trục tung nên x =0
(*)<=> m=-2m+3
=>3m=3
=>m=1
Đúng 3
Bình luận (0)
Để hai đồ thị cắt nhau tại 1 điểm trên trục tung thì \(m^2-1=8\)
\(\Leftrightarrow m^2=9\)
hay \(m\in\left\{3;-3\right\}\)
Đúng 1
Bình luận (0)
tìm K để 3 đường thẳng y=x+1y=-2x+4 và y=3x+k đồng quy
Tọa độ giao là:
-2x+4=x+1 và y=x+1
=>-3x=-3 và y=x+1
=>x=1 và y=2
Thay x=1 và y=2 vào y=3x+k, ta được:
k+3=2
=>k=-1
Đúng 0
Bình luận (0)
Cho ba đường thẳng
d
1
:
2
x
+
3
y
1
;
d
2
:
x
-
y
2
;
d
3
:
m
x
+
2
m
+
1
y
2
.Ba đường thẳng này đồng quy khi: A. m 12 B....
Đọc tiếp
Cho ba đường thẳng
d 1 : 2 x + 3 y = 1 ; d 2 : x - y = 2 ; d 3 : m x + 2 m + 1 y = 2 .
Ba đường thẳng này đồng quy khi:
A. m = 12
B. m = 13
C. m = 14
D. m = 15
Ba đường thẳng đã cho đồng quy khi hệ 2 x + 3 y = 1 x - y = 2 m x + ( 2 m + 1 ) y = 2 có nghiệm duy nhất.
Xét hệ gồm hai phương trình (1) và (2) :
2 x + 3 y = 1 ( 1 ) x - y = 2 ( 2 ) ⇔ 2 x + 3 y = 1 2 x - 2 y = 4 ⇔ 2 x + 3 y = 1 5 y = - 3 ⇔ x = 7 5 y = - 3 5
Hệ này có nghiệm duy nhất là 7 5 ; - 3 5 .
Để ba đường thẳng đã cho đồng quy thì 7 5 ; - 3 5 cũng là nghiệm của phương trình (3), tức là
m . 7 5 + 2 m + 1 . - 3 5 = 2 ⇔ 7 m - 3 2 m + 1 = 10 ⇔ 7 m - 6 m - 3 = 10 ⇔ m = 13 .
Đúng 0
Bình luận (0)
Cho 2 đường thẳng
y = (m^2 - 3)x + m - 1
y = x + 1
Tìm m để 2 đường thẳng đó:
a. song song
b. trùng nhau
b: Để hai đường thẳng trùng nhau thì \(\left\{{}\begin{matrix}m^2-3=1\\m-1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\m=2\end{matrix}\right.\Leftrightarrow m=2\)
Đúng 1
Bình luận (0)
Cho 2 đường thẳng
y = (m^2 - 3)x + m - 1
y = x + 1
Tìm m để 2 đường thẳng đó:
a. song song
b. trùng nhau
a: Để hai đường thẳng song song thì \(\left\{{}\begin{matrix}m^2-3=1\\m-1\ne1\end{matrix}\right.\Leftrightarrow m=-2\)
b: Để hai đường thẳng trùng nhau thì \(\left\{{}\begin{matrix}m^2-3=1\\m-1=1\end{matrix}\right.\Leftrightarrow m=2\)
Đúng 1
Bình luận (0)
Cho 2 đường thẳng
y = (m^2 - 3)x + m - 1
y = x + 1
Tìm m để 2 đường thẳng đó:
a. song song
b. trùng nhau
a, y = (m^2 - 3)x + m - 1 // y = x + 1
<=> \(\left\{{}\begin{matrix}m^2-3=1\\m-1\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\m\ne2\end{matrix}\right.\)
<=> m = \(\pm\)2 và \(m\ne2\)<=> m = -2
b, y = ( m^2 - 3 )x + m - 1 trùng y = x + 1
<=> \(\left\{{}\begin{matrix}m^2-3=1\\m-1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\m=2\end{matrix}\right.\)<=> m = 2
Đúng 1
Bình luận (0)
a: Để hai đường thẳng song song thì
\(\left\{{}\begin{matrix}m^2-3=1\\m-1\ne1\end{matrix}\right.\Leftrightarrow m=-2\)
b: Để hai đường thẳng trùng nhau thì
\(\left\{{}\begin{matrix}m^2-3=1\\m-1=1\end{matrix}\right.\Leftrightarrow m=2\)
Đúng 1
Bình luận (0)
1.a) Vẽ đồ thị hàm số y‐2x+3y‐2x+3 và tính góc của đường thẳng tạo với trục Ox b) Tìm m để đường thẳng yx+m2+1yx+m2+1 và đường thẳng y(m+1)x+5ym+1x+5 cắt nhau tại một điểm trên trục tung 2.Trong đợt quyên góp ủng hộ miền Trung bị bão lụt của trường THCS Đà Nẵng , lớp 9a và 9b quyên góp được 1105000 đồng .Mỗi học sinh lớp 9a đống góp 10000đồng , mỗi học sinh lớp 9b quyên góp 15000đồng .Gọi số học sinh lớp 9a là x và số học sinh lớp 9b là y a. em viết hệ thức biểu diễn y theo xb. nếu số học sinh...
Đọc tiếp
1.a) Vẽ đồ thị hàm số y=‐2x+3y=‐2x+3 và tính góc của đường thẳng tạo với trục Ox b) Tìm m để đường thẳng y=x+m2+1y=x+m2+1 và đường thẳng y=(m+1)x+5y=m+1x+5 cắt nhau tại một điểm trên trục tung 2.Trong đợt quyên góp ủng hộ miền Trung bị bão lụt của trường THCS Đà Nẵng , lớp 9a và 9b quyên góp được 1105000 đồng .Mỗi học sinh lớp 9a đống góp 10000đồng , mỗi học sinh lớp 9b quyên góp 15000đồng .Gọi số học sinh lớp 9a là x và số học sinh lớp 9b là y a. em viết hệ thức biểu diễn y theo xb. nếu số học sinh lớp 9a là 43 . tính số học sinh lớp 9b
a, Giải hệ phương trình:
x
+
1
y
-
1
x
y
-
1...
Đọc tiếp
a, Giải hệ phương trình: x + 1 y - 1 = x y - 1 x - 3 y - 3 = x y - 3
b, Trên mặt phẳng tọa độ Oxy, cho prabol (P): y = x 2 và đường thẳng d: y = 2 x + m 2 - 2 m . Tìm các giá trị của m để d cắt (P) cắt tại hai điểm phân biệt nằm về hai phía của trục tung Oy
a, Biến đổi hệ phương trình ban đầu ta được hệ x - y = 0 3 x + 3 y = 12
Từ đó tìm được x = 2, y = 2
b, Phương trình hoành độ giao điểm của d và (p):
x 2 - 2 x - m 2 + 2 m = 0 (1)
d cắt (P) tại hai điểm phân biệt nằm về hai phía của trục tung Oy <=> (1) có hai nghiệm trái dấu. Từ đó tìm được 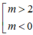
Kết luận 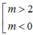
Đúng 0
Bình luận (0)











