
cần giúp, 3h là t ngủm rồi;-;
mong các bạn giúp mình ,mình cần gấp 3h hôm nay phải có rồi
(x+y):(5-z):(y+z):(y+9)=3:1:2:5
Ta có:
\(\frac{x+y}{3}=\frac{5-z}{1}=\frac{y+z}{2}=\frac{9+y}{5}=k\left(1\right)\)
\(\frac{\left(x+y\right)+\left(5-z\right)+\left(y+z\right)+\left(9+y\right)}{3+1+2+5}=\frac{x+y-4}{1}\)
=> \(\hept{\begin{cases}x+y-4=k\\x+y=3k\end{cases}}\)=> \(k+4=x+y\)
=> \(4+k=3k\Rightarrow4=2k\Rightarrow k=2\)
=> \(5-z=k\Rightarrow z=5-k=5-2=3\)
\(9+y=5k\Rightarrow y=5k-9=10-9=1\)
\(x+y=3k\Rightarrow x=3k-y=6-1=5\)
Từ (1) => \(\hept{\begin{cases}x=5\\y=1\\z=3\end{cases}}\)
\(\frac{x+y}{5-z}=\frac{3}{1}\Leftrightarrow x+y=15-3z\) (1)
\(\frac{5-z}{y+z}=\frac{1}{2}\Leftrightarrow10-2z=y+z\Leftrightarrow y=10-3z\) (2)
\(\frac{y+z}{y+9}=\frac{2}{5}\Leftrightarrow5y+5z=2y+18\Leftrightarrow3y=18-5z\) (3)
Tù (2) và (3), ta có HPT: \(\hept{\begin{cases}y=10-3z\\3y=18-5z\end{cases}}\)<=> \(\hept{\begin{cases}y+3z=10\\3y+5z=18\end{cases}}\)
Giải HPT đó, ta có: \(y=1\), \(z=3\)
Thay \(y=1\) và \(z=3\) vào PT(1), ta có: \(x=15-3\cdot3-1=15-9-1=5\)
Vậy \(x=5\), \(y=1\) và \(z=3\).
cảm ơn các bạn nha
 Ghi lại các từ láy và nêu tác dụng của các từ láy .
Ghi lại các từ láy và nêu tác dụng của các từ láy .
GIÚP MÌNH VỚI 3H LÀ MÌNH PHẢI NỘP RỒI
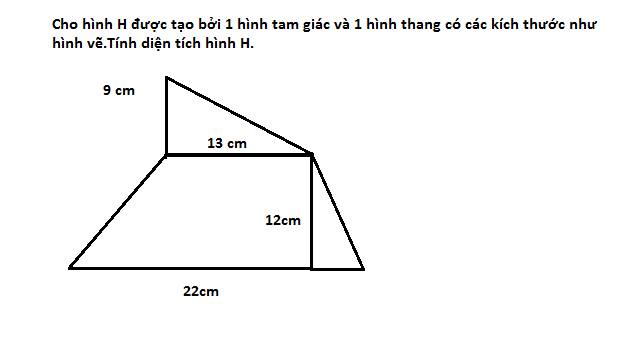
giúp em gấp với 3h phaie nộp rồi ạa;DD
Bài đã đăng rồi bạn lưu ý không đăng lặp lại nữa nhé.
Làm giúp em bài này với ạ, chiều 3h em học rồi. Em cảm ơn rất nhiều 🥲




giúp mik mấy bài này với mik cần rất gấp trước 3h nha
 giúp e 2 bài này với em cần gấp trước 3h chiều nay!!
giúp e 2 bài này với em cần gấp trước 3h chiều nay!!
(-19-137+54)-(63-46)
GIÚP MIK VỚI Ạ, CẦN TRC 3H Ạ
\(\left(-19-137+54\right)-\left(63-46\right)\)
\(=-19-137+54-63+46\)
\(=-19+\left(-137-63\right)+\left(54+46\right)\)
\(=-19+\left(-200\right)+100\)
\(=\left(-219\right)+100\)
\(=-119\)
1 xm lên dốc từ A - B với V 25km/h rồi trở về A với V gấp 2l V lúc đi. Biết T cả đi và về là 3h. Độ dài S ab là
Có ai ko giúp em với ạ .em đang cần gấp trước 3h a. Em cảm ơn