Trọng tâm của vật rắn trùng với tâm hình học của nó khi nào
A. Vật có dạng hình học đối xứng
B. Vật có dạng là một khối cầu
C. Vật đồng tính, có dạng hình học đối xứng
D. Vật đồng tính
Giải thích được trọng tâm của các vật phẳng, đồng chất, có dạng hình học đối xứng nằm ở tâm đối xứng của vật.
Học sinh tự tiến hành thí nghiệm theo cách làm ở phần trên để kiểm chứng kết luận: “Trọng tâm của các vật phẳng, mỏng và có dạng hình học đối xứng nằm ở tâm đối xứng của vật”.
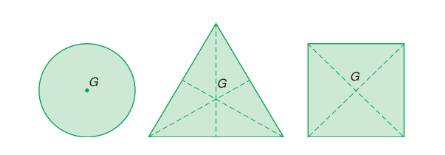
Cho biết trọng tâm của một số vật đồng chất và có dạng hình học đối xứng.
Đối với những vật phẳng mỏng có dạng hình học đối xứng: hình tròn tam giác đều, hình vuông, hình chữ nhật thì trọng tâm của vật là tâm đối xứng của vật (tâm hình tròn, giao điểm các đường phân giác, giao điểm hai đường chéo…).
Cho biết trọng tâm của một số vật đồng chất và có dạng hình học đối xứng?
Cách tính thể tích của các vật có hình dạng đối xứng trong toán học
Hình hộp chữ nhật: Lấy chiều cao nhân với chiều dài và chiều rộng
Hình hộp vuông : (quên cmn tên) lấy cạnh x cạnh x cạnh
Chọn phương án đúng. Trọng tâm của vật rắn
A. là một điểm nằn trên vật
B. trùng với tâm đối xứng của vật nếu vật phẳng mỏng
C. là điểm đặt của trọng lực
D. là nơi tập trung khối lượng của vật
c nha bạn chúc tất cả mọi người học giỏi nha ![]()
Hãy tìm một số hình ảnh, đồ vật trong tự nhiên có tính đối xứng (có trục đối xứng hoặc có tâm đối xứng).
Có ai biết cách tính thể tích của các vật có hình dạng đối xứng không ?
HHCN : Dài x Rộng x Cao
HLP : Cạnh x Cạnh x Cạnh
Chọn phương án sai. Trọng tâm của vật rắn
A. là điểm đặt của trọng lực
B. là một điểm xác định và có thể nằm ngoài vật
C. trùng với tâm đối xứng của vật nếu vật phẳng mỏng
D. nằm trên phương dây treo nếu vật cân bằng nhờ treo bởi một sợi dây
Số phát biểuđúng:
1. Qua phép vị tự có tỉ số k ≠ 0 , đường thẳng đi qua tâm vị tự sẽ biến thành chính nó
2. Qua phép vị tự có tỉ số k ≠ 0 , đường tròn có tâm là tâm vị tự sẽ biến thành chính nó.
3. Qua phép vị tự có tỉ số k ≠ 1 , không có đường tròn nào biến thành chính nó.
4. Qua phép vị tự V(O;1), đường tròn tâm O sẽ biến thành chính nó.
5. Phép vị tự tỉ số k biến đường thẳng thành đường thẳng song song hoặc trùng với đường thẳng đó
6. Phép vị tự tỉ số k biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với hệ số k
7. Trong phép vị tự tâm O, tỉ số k, nếu k < 0 thì điểm M và ảnh của nó ở về hai phía đối với tâm O.
8. Mọi phép dời hình đều là phép đồng dạng với tỉ số k = 1
9. Phép hợp thành của một phép vị tự tỉ số k và một phép đối xứng tâm là phép đồng dạng tỉ số
10. Hai đường tròn bất kì luôn có phép vị tự biến đường này thành đường kia
11. Khi k = 1 , phép vị tự là phép đồng nhất
12. Phép vị tự biến tứ giác thành tứ giác bằng nó
13. Khi k = 1, phép đồng dạng là phép dời hình
14. Phép đối xứng tâm là phép đồng dạng tỉ số k = 1
A.9
B.10
C.11
D.12
Đáp án C
Những phát biểuđúng: 1; 4; 5; 6; 7; 8; 9; 10; 11; 13; 14
2. Qua phép vị tự có tỉ số , đường tròn có tâm là tâm vị tự sẽ biến thành 1 đường tròn đồng tâm với đường tròn ban đầu và có bán kính = k. bán kính đường tròn ban đầu.
3. Qua phép vị tự có tỉ số đường tròn biến thành chính nó.
12. Phép vị tự với tỉ số k = biến tứ giác thành tứ giác bằng nó