Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng AM<\(\frac{AB+AC}{2}\)

Những câu hỏi liên quan
Cho tam giác ABC. Gọi M là trung điểm của BC.
Chứng minh rằng A M < A B + A C 2
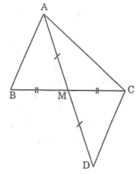
Trên tia đối của tia MA lấy điểm D sao cho MA = MD.
Xét ΔAMB và ΔDMC, ta có:
MA = MD (theo cách vẽ)
∠(AMB) = ∠(DMC) (đối đỉnh)
MB = MC (gt)
Suy ra: ΔAMB = ΔDMC (c.g.c)
Suy ra: AB = CD (hai cạnh tương ứng)
Trong ΔACD, ta có: AD < AC + CD
(bất đẳng thức tam giác)
Suy ra: AD < AC + AB
Mà AD = AM + MD = 2AM
Suy ra: 2AM < AC + AB hay 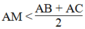
Đúng 0
Bình luận (0)
cho tam giác ABC có AB = AB . Gọi M là trùn điểm của BC . Chứng minh rằng :
a, AM là phân giác của góc BAC.
b, Am là trung trực của BC.
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
=>AM là phân giác của góc BAC
b: ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có:MB=MC
=>M nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AM là đường trung trực của BC
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA=MD.
a) Chứng minh rằng tam giác ABM= tam giác DCM.
b) Gọi K là trung điểm của AC. Chứng minh rằng BK=DK.
c) Gọi E là giao điểm của AM và BK, F là giao điểm Của KD và BC. Chứng minh rằng tam giác KEF cân
1 ) Cho tam giác ABC . Gọi M là một điểm nằm trong tam giác . Chứng minh rằng : MA + MB + MC > nửa chu vi tam giác đó
2 ) Cho tam giác ABC . Gọi M là trung điểm cạnh BC . Chứng minh rằng : AM < AB + AC / 2
Cho tam giác ABC cân tại A ( AB > BC).
Gọi M là trung điểm của BC, H là trung điểm của AM.
a. Chứng minh rằng tam giác AMB bằng tam giác AMC. Chứng minh AM ⊥ BC
b.Tính độ dài đoạn AM nếu BC = 6cm; AB = 8cm
c. Đường thẳng qua A song song với BC cắt tia BH và CH lần lượt tại E và F. Chứng minh A là trung
điểm của EF
mk cần hình và lời giải chi tiết nha
các pro giúp mk với
Đúng 0
Bình luận (0)
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: BC=6cm nên BM=3cm
Xét ΔABM vuông tại M có \(AB^2=AM^2+MB^2\)
hay \(AM=\sqrt{55}\left(cm\right)\)
Đúng 1
Bình luận (1)
cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC
a, chứng minh rằng tam giác AMB= tam giác AMC
b, chứng minh rằng AM là tia phân giác của góc BC
a) Xét ΔAMB và ΔAMC , có:
\(\hept{\begin{cases}AM-chung\\AB=AC\left(gt\right)\\MB=MC\left(TĐBC\right)\end{cases}}\)( TĐBC : trung điểm BC nha )
\(\Rightarrow\Delta AMB=\Delta AMC\left(c.c.c\right)\)
b) Ta có :^BAM = ^MAC ( \(\Delta\)AMB = \(\Delta\)AMC )
=> AM là tia phân giác của ^BAC
Cho tam giác ABC có canh AB=AC. Gọi M là trung điểm của BC.
a) Chứng minh rằng: góc ABC= góc ACB
b) Chứng minh rằng: AM là tia phân giác của góc BAC
c) Chứng minh rằng AM vuông góc với BC
cho tam giác ABC có AB=AC. Gọi M là trung điểm của BC. Chứng minh rằng: a) tam giác AMB= tam giác AMC b) AM là tia phân giác của BAC c) AM vuông góc với BC d) Vẽ At là tia phân giác của góc ngoài ở đỉnh A của tam giác ABC . Chứng minh : At // BC
Cho tam giác ABC, gọi N là trung điểm của AC. Trên tia đối của tia NB, lấy điểm M sao cho NB = NM. Chứng minh rằng :
a) Tam giác ABN = tam giác CMN
b) AM // BC
c) Gọi P là trung điểm của BC, Q là trung điểm của AM. Chứng minh rằng ba điểm P, N, Q thẳng hàng
Bạn chỉ cần giải giúp mình câu c) là được !
ta có : góc CNA =180 đô
mà :CNP = góc ANQ (đôí đỉnh)
suy ra :góc PNQ = góc PNA +góc ANQ - góc CNP =180 (góc bẹt)
vâỵ : P,N,Q thăng hàng.
Đúng 0
Bình luận (0)
Cho tam giác ABC, gọi I là trung điểm của AB. Trên tia đối của IC lấy M sao cho IM=IC.
a) Chứng minh rằng tam giác AIM = tam giác BIC. Từ đó suy ra AM=BC và AM//BC.
b) Gọi E là trung điểm của AC, trên tia đối của EB lấy N sao cho EN=EB. Chứng minh AN//BC.
c) Chứmg minh: M,A,N thẳng hàng và A là trung điểm của MN.
a: Xét ΔAIM và ΔBIC có
IA=IB
\(\widehat{AIM}=\widehat{BIC}\)
IM=IC
Do đó: ΔAIM=ΔBIC
=>\(\widehat{IAM}=\widehat{IBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AM//BC
ΔIAM=ΔIBC
=>AM=BC
b: Xét ΔEAN và ΔECB có
EA=EC
\(\widehat{AEN}=\widehat{CEB}\)
EN=EB
Do đó: ΔEAN=ΔECB
=>\(\widehat{EAN}=\widehat{ECB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AN//CB
c: ΔEAN=ΔECB
=>AN=CB
AN//CB
AM//CB
AN,AM có điểm chung là A
Do đó: M,A,N thẳng hàng
mà MA=NA
nên A là trung điểm của MN
Đúng 3
Bình luận (0)
















