Trục đối xứng của parabol ( P ) : y = − 2 x 2 + 5 x + 3 là
A. x = - 5 2
B. x = - 5 4
C. x = 5 2
D. x = 5 4
Trục đối xứng của parabol y = ( x 2 / 5 ) + 2 x + 7 là
A. y = -3 B. y = -5
C. x = -5 D. x = 5
Đáp án: C (trục đối xứng là đường thẳng x = (-b)/2a).
tìm parabol y=ax2+bx+3 biết rằng parabol đó có trục đối xứng là x=-2 và đỉnh của parabol có tung độ bằng 19.
Lời giải:
Theo bài ra thì tọa độ đỉnh của parabol là $(-2,19)$
Từ hàm $y=ax^2+bx+3=a(x+\frac{b}{2a})^2+3-\frac{b^2}{4a}$ ta có tọa độ đỉnh của parabol là:
$(\frac{-b}{2a}, 3-\frac{b^2}{4a})$
$\Rightarrow \frac{-b}{2a}=-2; 3-\frac{b^2}{4a}=19$
$\Rightarrow a=-4; b=-16$
1.Tìm pt parabol y=ax2+bx +3(a≠0)khi biết:
a. Hàm số y=f(x) đạt cực đại bằng 12 tại x=3
b. Parabol tiếp xúc với trục hoành tại x=-1
c. Parabol cắt trục hoành tại hai điểm M(-1;0)và N(-3;0)
d. Parabol qua điểm E(-1;9)và có trục đối xứng là x=-2
2. Xác định hàm số bậc 2 y=ax2+ bx+c(a≠0)biết rằng:
a. Hàm số triệt tiêu khi x=8 và đạt cực tiểu bằng -12 khi x=6
b. Hàm số có giá trị bằng -3 khi x= -1 và đạt cực đại bằng 13/4 khi x=3/2
3. Tìm pt của parabol y= ax2+bx+c(a≠0) biết:
a. Parabol qua 2 điểm A(2;-5);B(-1;16) và có trục đối xứng x=4
b. Parabol cắt trục hoành tại C(1;0) cắt trục tung tại D(0;5) và có trục đối xứng x=3
Tìm parabol (P): y = ax2 + 3x – 2 biết rằng có trục đối xứng x = -3.
A. y = x2 + 3x – 2.
B. 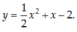
C. ![]()
D. 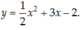
Vì parabol (P) có trục đối xứng x = -3 nên:
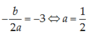
Chọn D.
Xác định trục đối xứng, tọa độ đỉnh, giao điểm với trục tung và trục hoành của parabol.
y = 2 x 2 - x - 2
Ở đây a = 2; b = -2; c = -2. Ta có Δ = ( - 1 ) 2 - 4 . 2 . ( - 2 ) = 17
Trục đối xứng là đường thẳng x = 1/4; đỉnh I(1/4; -17/8) giao với trục tung tại điểm (0; -2).
Để tìm giao điểm với trục hoành ta giải phương trình
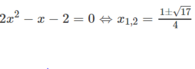
Vậy các giao điểm với trục hoành là

Xác định trục đối xứng, tọa độ đỉnh, giao điểm với trục tung và trục hoành của parabol.
y = - 2 x 2 - x + 2
Trục đối xứng x = -1/4; đỉnh I(-1/4; -17/8) giao với trục tung tại điểm (0;2); giao với trục hoành tại các điểm
![]()
Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó: Đi qua hai điểm A(3; -4) và có trục đối xứng là x = -3/2
+ Parabol y = ax2 + bx + 2 có trục đối xứng x = –3/2
⇒ –b/2a = –3/2 ⇒ b = 3a (1)
+ Parabol y = ax2 + bx + 2 đi qua điểm A(3; –4)
⇒ –4 = a.32 + b.3 + 2 ⇒ 9a + 3b = –6 (2).
Thay b = 3a ở (1) vào biểu thức (2) ta được:
9a + 3.3a = –6 ⇒ 18a = –6 ⇒ a = –1/3 ⇒ b = –1.
Vậy parabol cần tìm là y = –1/3x2 – x + 2.
Xác định Parabol (P): y = ax 2 + b x − 5 biết rằng Parabol đi qua điểm A (3; -4)và có trục đối xứng x = - 3 2
A. y = 1 18 x 2 + 1 6 x − 5
B. y = 1 18 x 2 + 1 6 x + 5
C. y = 3 x 2 + 9 x − 9
D. y = − 1 18 x 2 + 1 6 x − 5
xác định phương trình parabol (P) : y = x^2 + bx + c biết rằng c = 2, (P) đi qua (3;-4) và có trục đối xứng x = -3/2
Lời giải:
$(P):y=x^2+bx+2$ đi qua $(3;-4)$ nên:
$-4=3^2+b.3+2\Rightarrow b=-5$
Vậy pt cần tìm là $y=x^2-5x+2$
Vậy thì trục đối xứng $x=\frac{-3}{2}$ có vẻ thừa?
Xác định parabol y = 3x^2+bx+c, biết rằng parabol đó đi qua A(2;19) và nhận đường thẳng x = -2/3 làm trục đối xứng.
Lời giải:
Parabol đi qua $A(2;19)$ nên $y_A=3x_A^2+bx_A+c$ hay $19=12+2b+c$
$\Rightarrow 2b+c=7(1)$
$x=\frac{-2}{3}$ là trục đối xứng
$\Leftrightarrow \frac{-b}{2.3}=\frac{-2}{3}$
$\Rightarrow b=4(2)$
Từ $(1); (2)\Rightarrow c=-1$
Vậy parabol có pt $y=3x^2+4x-1$
Theo đề, ta có:
\(\left\{{}\begin{matrix}\dfrac{-b}{6}=\dfrac{-2}{3}\\12+2b+c=19\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=4\\c=-1\end{matrix}\right.\)