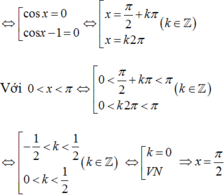Giải phương trình: cos2( π 3 + x) + 4cos( π 6 – x) = 4
A. x = ± π 6 + k2π, k ∈ Z
B. x = ± 5 π 6 + k2π, k ∈ Z
C. x = π 6 + k2π, k ∈ Z
D. Đáp án khác
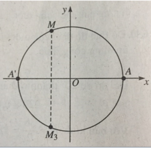
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π/2 < α < π, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 3 là
A. π - α + k2π, k ∈ Z B. α + π/2 + k2π, k ∈ Z
C. α - π + k2π, k ∈ Z D. -α + k2π, k ∈ Z
-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.
Vậy (-5π)/2 < -6,32 < -2π.
Do đó điểm M nằm ở góc phần tư thứ II.
Đáp án: B
Hai chất điểm A và B dao động trên hai trục của hệ tọa độ Oxy (O là vị trí cân bằng của 2 vật) với phương trình lần lượt là x = 4cos(10πt + π/6) cm và x = 4cos(10πt + π/3) cm. Khoảng cách lớn nhất giữa A và B là
A. 5,86cm
B. 5,26cm
C. 5,46cm
D. 5,66cm
Đáp án C
Phương pháp : Khoảng cách giữa hai vật ∆x = x1 – x2
Cách giải :
![]()
Vậy khoảng cách lớn nhất là 5,46cm
Cho hai dao động điều hoà cùng phương có các phương trình lần lượt là x 1 = 4cos( π t - π /6)(cm) và x 2 = 4cos(π π t - π /2)(cm). Dao động tổng hợp của hai dao động này có biên độ là
A. 8 cm. B. 2 cm. C. 4 3 . D. 4 2 .
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π < α < 3π/2, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 2 là
A. α - π + k2π, k ∈ Z B. π - α + k2π, k ∈ Z
C. 2π - α + k2π, k ∈ Z D. 3π/2 - α + k2π, k ∈ Z
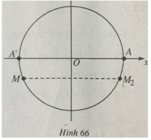
(h.66) Ta có
A M 2 = MA’ = MA + AA’
Suy ra
Sđ A M 2 = -α + π + k2π, k ∈ Z.
Vậy đáp án là B.
6.13. (h.67) Ta có
Sđ A M 3 = -sđ AM = -α + k2π, k ∈ Z.
Đáp án: D
Hai chất điểm A và B dao động trên hai truc̣ của hệ tọa độ Oxy( O là vị trí cân bằng của 2 vật) với phương trình lần lượt là: x=4cos(10πt+π/6)cm và y=4cos(10πt+φ)cm. Biết –π/2 <φ<π/2. Để khoảng cách AB không đổi thì giá trị của φ bằng
A. π/6
B. – π/3
C. 5π/6
D. π/3
Đáp án B
Phương pháp: Sử dụng định lý Py-ta-go và lí thuyết về dao động điều hòa
Cách giải :
Khoảng cách giữa hai chất điểm A và B được xác định theo công thức: d = x 2 + y 2
Theo đề bài ta có:
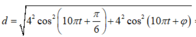
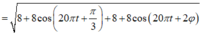
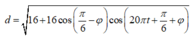
=> Để khoảng cách giữa AB không thay đổi thì khoảng cách này phải không phụ thuộc vào t
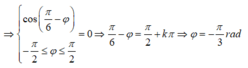
giải các phương trình sau
a/ \(^{tan^2x-\frac{4}{cotx}+=0}\)
b/\(cos2\left(x+\frac{\text{π}}{3}\right)+4cos\left(\frac{\text{π}}{6}-x\right)=\frac{5}{2}\)
c/\(\frac{1}{cos^2x}-1+tanx-\sqrt{3}\left(tanx+1\right)=0\)
d/tanx-2cotx+1=0
Mọi người ơi giúp mình với <3 cảm ơn mọi người nhìu ạ
Bạn ghi đề chính xác ra đi, câu a và câu b đó bạn
Câu a sau \(\frac{4}{cotx}\) còn dấu + nhưng không biết cộng với cái gì
Câu b biểu thức cos đầu tiên là \(cos^2\left(x+\frac{\pi}{3}\right)\) hay \(cos\left(2x+\frac{2\pi}{3}\right)\)
a) Đề thiếu
b)
PT $\Leftrightarrow 1-2\sin^2(x+\frac{\pi}{3})+4\cos (\frac{\pi}{6}-x)-\frac{5}{2}=0$
$\Leftrightarrow 1-2\sin ^2[\frac{\pi}{2}-(\frac{\pi}{6}-x)]+4\cos (\frac{\pi}{6}-x)-\frac{5}{2}=0$
$\Leftrightarrow -2\cos ^2(\frac{\pi}{6}-x)+4\cos (\frac{\pi}{6}-x)-\frac{3}{2}=0$
$\Leftrightarrow -2t^2+4t-\frac{3}{2}=0$ với $t=\cos (\frac{\pi}{6}-x)$
Đến đây bạn giải pt bậc 2 thu được $\cos (\frac{\pi}{6}-x)=\frac{1}{2}$
$\Rightarrow x=2k\pi +\frac{\pi}{2}$ hoặc $x=2k\pi -\frac{\pi}{6}$ với $k$ nguyên
c)
ĐK:.............
PT $\Leftrightarrow 1+\frac{\sin ^2x}{\cos ^2x}-1+\tan x-\sqrt{3}(\tan x+1)=0$
$\Leftrightarrow \tan ^2x+\tan x-\sqrt{3}(\tan x+1)=0$
$\Leftrightarrow \tan ^2x+(1-\sqrt{3})\tan x-\sqrt{3}=0$
$\Rightarrow \tan x=\sqrt{3}$ hoặc $\tan x=-1$
$\Rightarrow x=\pi (k-\frac{1}{4})$ hoặc $x=\pi (k+\frac{1}{3})$ với $k$ nguyên
d)
ĐK:.......
PT $\Leftrightarrow \tan x-\frac{2}{\tan x}+1=0$
$\Leftrightarrow \tan ^2x+\tan x-2=0$
$\Leftrightarrow (\tan x-1)(\tan x+2)=0$
$\Rightarrow \tan x=1$ hoặc $\tan x=-2$
$\Rightarrow x=k\pi +\frac{\pi}{4}$ hoặc $x=k\pi +\tan ^{-2}(-2)$ với $k$ nguyên.
Cho hai dao động điều hòa cùng phương có các phương trình lần lượt là x 1 = 4 cos π t - π 6 ( c m ) và x 2 = 4 cos π t - π 2 ( c m ) . Dao động tổng hợp của hai dao động này có biên độ là
A. 2 cm
B. 4 2 c m
C. 8 cm
D. 4 3 c m
Đáp án D
Ta có:
A 2 = A 1 2 + A 2 2 + 2 A 1 A 2 cos ( φ 1 - φ 2 ) = 48
Tính:F=Cos(π/4+α) x cos(π/4-α)
G=Sin(π/3+α) x cos(π/3-α)
H=cos(π/2-α) x sin(π/2+α)
I=sin(π/4+α) - cos(π/4-α)
K=cos(π/6-x) - sin(π/3+x)
Nghiệm của phương trình cos2 x- cosx = 0 thỏa mãn điều kiện 0 < x < π
A. x= π / 6
B. x= π / 2
C. x= π / 4
D. x=- π / 2
Hướng dẫn giải
Chọn B.
Ta có : cos2 x- cosx = 0 ó cosx. ( cosx – 1) = 0