Số - 2 3 được biểu diễn trên trục số bởi hình vẽ nào sau đây:
A. 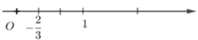
B. 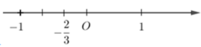
C. 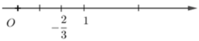
D. 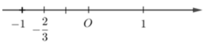
Số 3 2 được biểu diễn trên trục số bởi hình vẽ nào sau đây:
A. 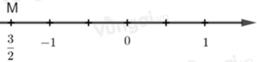
B. 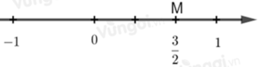
C. 
D. 
+ Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành 2 phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng 1 2 đơn vị cũ.
+ Số 3 2 được biểu diễn bởi điểm M nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 3 đơn vị mới.

Đáp án cần chọn là: D
Số -2/3 được biểu diễn trên trục số bằng hình vẽ nào dưới đây?
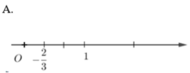
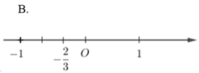
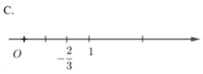
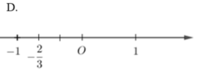
Biểu diễn số -2/3 trên trục số ta được hình vẽ:
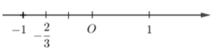
Chọn đáp án D.

câu 15. Cho 4 số nguyên lần lượt có điểm biểu diễn trên trục số là A B C D , , , được cho như hình vẽ dưới đây:
Câu 15. Cho 4 số nguyên lần lượt có điểm biểu diễn trên trục số là A B C D , , , được cho như hình vẽ dưới đây:

Nam vẽ một phần trục số trên vở ô li và đánh dấu ba điểm A, B,C như sau:

a) Hãy cho biết hai điểm A,B biểu diễn những số thập phân nào?
b) Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác 0,05.
Mỗi đơn vị được chia thành 10 phần bằng nhau nên khoảng cách giữa 2 vạch chia liên tiếp là 0,1 đơn vị.
a) Điểm A biểu diễn số 13,4
Điểm B biểu diễn số 14,2
b) Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác 0,05, ta được 14,6 (vì điểm C nằm gần vạch biểu thị số 14,6 nhất).
Câu 15. Cho 4 số nguyên lần lượt có điểm biểu diễn trên trục số là A B C D , , , được cho như hình vẽ dưới đây:

Tổng của 4 số đó là A. −1.
B. 9.
C. 0.
D. −3.
Hình vẽ bên biểu diễn trục hoành cắt đồ thị y = f(x) tại ba điểm có hoành độ 0 , a , b a < 0 < b . Gọi S là hình phẳng giới hạn bởi đồ thị y = f(x) và trục hoành, khẳng định nào sau đây sai?
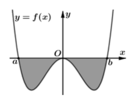
A. S = - ∫ a 0 f x d x + ∫ 0 b f x d x
B. S = ∫ a 0 f x d x + ∫ 0 b f x d x
C. S = ∫ a 0 f x d x + ∫ 0 b f x d x
D. S = ∫ 0 b f x d x
Cho hàm số y = f(x) liên tục trên đoạn [a;b] và cắt trục hoành tại điểm x = c (như hình vẽ). Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b. Khẳng định nào sau đây là khẳng định đúng?
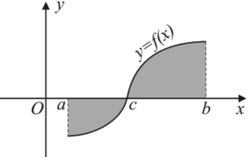
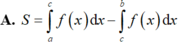
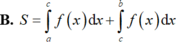
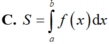
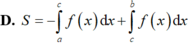
Chọn D
Ta có
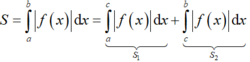
Vì f(x) < 0, ∀ x ∈ a ; c nên |f(x)| = –f(x).
Do đó, S 1 = - ∫ a c f x d x .
Tương tự, f(x) > 0, ∀ x ∈ a ; c nên |f(x)| = f(x).
Do đó, S 2 = ∫ c b f x d x .
Vậy S = - ∫ a c f x d x + ∫ c b f x d x .
a) Các điểm A,B,C trong Hình 8 biểu diễn số hữu tỉ nào?
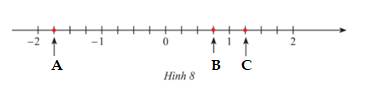
b) Biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số.
a) Các điểm A,B,C trong Hình 8 biểu diễn lần lượt các số hữu tỉ: \(\frac{{ - 7}}{4};\,\frac{3}{4};\,\frac{5}{4}.\)
b) Ta có: \(1\frac{1}{5} = \frac{6}{5};\,\,\, - 0,8 = \frac{{ - 8}}{{10}} = \frac{{ - 4}}{5}.\)
Vậy ta biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số như sau:
