Cho hình hộp chữ nhật ABCD. A^’B^’C^’D^’ có O và O^’ lần lượt là tâm ABCD; A^’B^’C^’D^’. Chọn kết luận đúng

A. Hai mp (ACC^’A^’) và mp (BDD^’B^’) cắt nhau nhau theo đường thẳng OO^’

B. Hai mp (ADD^’A^’) và mp (BDD^’B^’) cắt nhau nhau theo đường thẳng BD^’

C. Hai mp (ACC^’A^’) và mp (BDD^’B^’) cắt nhau nhau theo đường thẳng AA^’

D. Hai mp (ACC^’A^’) và mp (BDD^’B^’) song song

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có A B = B C = 1 2 A A '  Gọi O,O’ lần lượt là tâm hai đáy ABCD và A’B’C’D’, M là điểm thỏa mãn M O → = - 1 2 M O ' →  Giá trị tan góc giữa hai mặt phẳng (MAB) và (MAD) bằng

A.  3

B.  6 3

C.  3 3

D.  4 3 3

Cho hình hộp chữ nhật ABCD. A’B’C’D’  có diện tích các mặt ABCD, BCC’B’, CDD’C’ lần lượt là 2 a 2 ,   3 a 2 ,   6 a 2 . Tính thể tích khối hộp chữ nhật ABCD. A’B’C’D’

A.  36 a 3

B.  6 a 3

C.  36 a 6

D.  6 a 2

Cho hình lập phương ABCD.A’B’C’D’. Gọi O, O’ lần lượt là tâm của hai hình vuông ABCD và A’B’C’D’. Gọi V₁ là thể tích của khối trụ xoay có đáy là 2 đường tròn ngoại tiếp hình vuông ABCD và A’B’C’D’, V₂ là thể tích khối nón tròn xoay đỉnh O và có đáy là đường tròn nội tiếp hình vuông A’B’C’D’. Tỷ số thể tích V 1 V 2 là

A. 4

B. 8 

C. 6

D. 2

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh a và cạnh bên bằng 3a. Diện tích xung quanh S_xq của hình nón có đỉnh là tâm O của hình vuông A’B’C’D’ có đáy là hình tròn nội tiếp hình vuông ABCD là

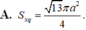
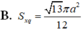
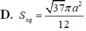
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh a, AA’ = 2a. Một hình trụ có hai đáy là hai hình tròn lần lượt ngoại tiếp hình vuông ABCD và hình vuông A’B’C’D’. Tính diện tích xung quanh S x q  của hình trụ đó

A.  S x q = 2 πa 2

B.  S x q = 2 πa 2 2

C.  S x q = 4 πa 2 2

D.  S x q = πa 2 2

Cho hình hộp ABCD. A’B’C’D’ gọi O  là giao điểm của AC và BD. Tính tỉ số thể tích của khối chóp O. ABC và khối hộp ABCD. A’B’C’D’ điểm của AC và BD. Tính tỉ số thể tích của khối chóp O. ABC và khối hộp ABCD. A’B’C’D’

A.  1 4

B.  1 3

C.  1 6

D.  1 12

Cho hình hộp chữ nhật ABCD. A’B’C’D’ có thể tích bằng 1 và G là trọng tâm tam giác BCD’ Thể tích V của khối chóp G. ABC’ là

A.  V   =   1 3

B.  V   =   1 6

C.  V   =   1 12

D.  V   =   1 18

Cho hình hộp chứ nhật ABCD.EFGH với AB = 12cm; BC = 9cm; AE = 10cm.

          a) Tính diện tích toàn phần và thể tích hình hộp chữ nhật ABCD.EFGH

          b) Gọi O và I lần lượt là tâm đối xứng của hình chữ nhật EFGH và ABCD. Đường thẳng OI song song với những mặt phẳng nào?

          c) Tính diện tích xung quanh của hình chóp OABCD.