
Những câu hỏi liên quan
cho đường tròn tâm O dây AB không đi qua tâm ,N và M là điểm chính giữa cung AB lớn và nhỏ.
a)Chứng minh MN là đường trung trực của dây AB
b)Chứng minh3 điểm M,O,N thẳng hàng
cho (O;R) vẽ dây AB khác đường kính . M trung điểm AB,OM cắt đường tròn tại E . Chứng tỏ E là điểm chính giữa cung nhỏ AB
Hình bạn tự vẽ nhé :
Xét \(\Delta\)OAB có : OA=OB=R \(\Rightarrow\Delta\)OAB cân tại O ⇒ OM là đường trung tuyến đồng thời là đường phân giác ⇒ góc MOA= góc MOB ⇒ góc EOA= góc EOB Lại có góc EOA = số đo cung EA; góc EOB = số đo cung EB ⇒ số đo cung EA = số đo cung EB \(\Rightarrow\) E là điểm chính giữa của cung AB
Đúng 1
Bình luận (0)
Cho đường tròn (O). Gọi I là điểm chính giữa của cung AB (không phải là cung nửa đường tròn) và H là trung điểm của dây AB. Chứng minh rằng đường thẳng IH đi qua tâm O của đường tròn ?
Vì I là điểm chính giữa của cung AB nên IA=IB
=>I nằm trên đường trung trực của AB(1)
Ta có: HA=HB
nên H nằm trên đường trung trực của AB(2)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(3)
Từ (1), (2) và (3) suy ra O,H,I thẳng hàng
Đúng 0
Bình luận (0)
Cho đường tròn tâm O.Gọi I là điểm chính giữa của cung AB (không phải là cung nửa đường tròn) và H là trung điểm của dây AB .Chứng minh rằng đường thẳng IH đi qua tâm O của đường tròn
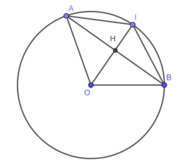
Suy ra : IA =IB (hai cung bằng nhau căng hai dây bằng nhau)
Hay I nằm trên đường trung trực của AB
Mà OA =OB (=R)
Nên O nằm trên đường trung trực của AB
Suy ra OI là đường trung trực của AB
Vì H là trung điểm của AB nên OI đi qua trung điểm H
Vậy ba điểm I, H, O thẳng hàng
Đúng 0
Bình luận (0)
Cho đường tròn (O) đường kính AB. Vẽ dây CD vuông góc với đường kính AB tại H. Gọi M là điểm chính giữa cung nhỏ CB, I là giao điểm của CB và OM. Chứng minh: Bốn điểm O,H,C,I cùng nằm trên 1 đường tròn.
OB=OC
MB=MC
=>OM là trung trực của BC
=>OM vuông góc BC tại I
góc CHO+góc CIO=180 độ
=>CHOI nội tiếp
Đúng 0
Bình luận (0)
Cho AB là dây cung của (O) và đường thăng xAy là tiếp tuyến của (O). Kẻ OM vuông góc AB ở M và cắt xAy ở C. 1) Chứng minh: OC là đường trung trực của AB. 2) Chứng minh: CB là tiếp tuyến của (O) 3) Kẻ đường kính BD. Chứng minh AD//OA
1: ΔOAB cân tại O
mà OM là đường cao
nên OM là trung trực của AC
=>OC là trung trực của AB
2: ΔOAB cân tại O
mà OM là đường cao
nên OM là phân giác của góc AOB
Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
=>ΔOAC=ΔOBC
=>góc OBC=90 độ
=>CB là tiếp tuyến của (O)
3: Sửa đề: CM AD//OC
Xét (O) có
góc DAB là góc nội tiếp chắn nửa đường tròn
=>góc DAB=90 độ
=>DA vuông góc AB
=>DA//OC
Đúng 1
Bình luận (0)
Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.
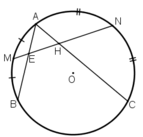
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 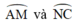
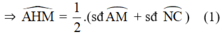
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 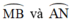
+ Do M và N là điểm chính giữa của cung A B ⏜ v à A C ⏜
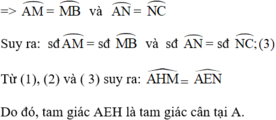
Đúng 1
Bình luận (0)
Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.
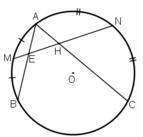
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung ![]()
![]()
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 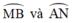

Kiến thức áp dụng
+ Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Đúng 0
Bình luận (0)
Cho nữa đường tròn (O;R) đường kính AB. Lấy điểm C là điểm chính giữa của cung AB, N là trung điểm của dây cung CB. Đường thẳng AN cắt nữa đường tròn (O) tại M. Từ C kẻ CI vuông góc với AM tại I.
a) Chứng minh tứ giác ACIO nội tiếp.
b) Chứng minh góc MOI = góc CAI.
c) Tính bán kính đường tròn ngoại tiếp tam giác IOM theo R.













