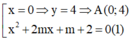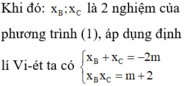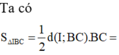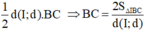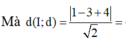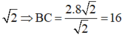\(\hept{\begin{cases}\frac{x-3}{2}=\frac{y-4}{3}=\frac{z+5}{4}\\x-3y+z=8\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x-3}{2}=\frac{3\left(y-4\right)}{3\cdot3}=\frac{z+5}{4}\\x-3y+z=8\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x-3}{2}=\frac{3y-12}{9}=\frac{z+5}{4}\\x-3y+z=8\end{cases}}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(...=\frac{x-3-\left(3y-12\right)+z+5}{2-9+4}=\frac{x-3-3y+12+z+5}{2-9+4}=\frac{\left(x-3y+z\right)-3+12+5}{2-9+4}=\frac{8-3+12+5}{2-9+4}=-\frac{22}{3}\)

\(\frac{x-3}{2}=-\frac{22}{3}\Rightarrow x-3=-\frac{44}{3}\Rightarrow x=-\frac{35}{3}\)

\(\frac{y-4}{3}=-\frac{22}{3}\Rightarrow y-4=-22\Rightarrow y=-18\)

\(\frac{z+5}{4}=-\frac{22}{3}\Rightarrow z+5=-\frac{88}{3}\Rightarrow z=-\frac{103}{3}\)

Vậy ...

A=2(x+y)+3xy(x+y)+5x²y²(x+y)+2

A=2.0+3xy.0+5x²y².0+2

A=2

B=xy(x+y)+2x²y (x+y)+5

B=xy.0+2x²y.0+5=5

a,Ta có 2(x+y)+3xy(x+y)+5x²y²(x+y)+4

Xg thay x+y=0 vào là dc bn nhó

Chúc bn hok tốt

Biến đổi mỗi đa thức theo hướng làm xuất hiện thừa số x+y-2 \(M=x^3+x^2y-2x^2-xy-y^2+3y+x-1\)

\(M=x^3+x^2y-2x^2-xy-y^2+\left(2y+y\right)+x-\left(-2+1\right)\)

\(M=\left(x^3+x^2y-2x^2\right)-\left(xy+y^2-2y\right)+\left(x+y-2\right)+1\)

\(M=\left(x^2.x+x^2.y-2x^2\right)-\left(x.y+y.y-2y\right)+\left(x+y-2\right)+1\)

\(M=x^2.\left(x+y-2\right)-y.\left(x+y-2\right)+\left(x+y-2\right)+1\)

\(M=x^2.0+y.0+0+1\)

\(M=1\)

\(N=x^3+x^2y-2x^2-xy^2+x^2y+2xy+2y+2x-2\)

\(N=x^3+x^2y-2x^2-xy^2+x^2y+2xy+2y+2x-\left(-4+2\right)\)

\(N=\left(x^3+x^2y-2x^2\right)-\left(x^2y+xy^2-2xy\right)+\left(2x+2y-4\right)+2\)

\(N=\left(x^2x+x^2y-2x^2\right)-\left(xyx+xyy-2xy\right)+\left(2x+2y-4\right)+2\)

\(N=x^2\left(x+y-2\right)-xy\left(x+y-2\right)+2\left(x+y-2\right)+2\)

\(N=x^2.0-xy.0+2.0+2\)

\(N=2\)

\(P=x^4+2x^3y-2x^3+x^2y^2-2x^2y-x\left(x+y\right)+2x+3\)

\(P=\left(x^4+x^3y-2x^3\right)+\left(x^3y+x^2y^2-2x^2y\right)-\left(x^2+xy-2x\right)+3\)\(P=\left(x^3x+x^3y-2x^3\right)+\left(x^2y.x+x^2yy-2x^2y\right)-\left(xx+xy-2x\right)+3\)

\(P=x^3\left(x+y-2\right)+x^2y\left(x+y-2\right)-x\left(x+y-2\right)+3\)

\(P=x^3.0+x^2y.0-x.0+3\)

\(P=3\)

Tích mình nha!

Mà bài này hình như học ở lớp 7 rồi!

Lời giải:

$x+y-2=0\Rightarrow x+y=2$

a) 

$B=x^4+2x^3y-2x^3+x^2y^2-2x^2y-x(x+y)+2x+3$

$=x^3(x+y)+x^3y-2x^3+x^2y^2-2x^2y-2x+2x+3$

$=2x^3+x^3y-2x^3+x^2y^2-2x^2y+3$

$=x^3y+x^2y^2-2x^2y+3$

$=xy(x^2+xy-2x)+3=xy[x(x+y)-2x]+3=xy(2x-2x)+3=3$

b) 

$C=x^3+x^2y-2x^2-xy+y^2-3y-x+5$

$=x^2(x+y)-2x^2-xy+y^2-3(y+x)+2x+5$

$=2x^2-2x^2-xy+y^2-6+2x+5$

$=-xy+y^2+2x-1$

$=y(x+y)+2x-1-2xy=2y+2x-1-2x=2(x+y)-1-2x=3-2x$ (không tính cụ thể được giá trị- bạn xem lại đề)

c) 

$D=2x^4+3x^2y^2+y^4+y^2$

$=(x^4+2x^2y^2+y^4)+x^4+x^2y^2+y^2

$=(x^2+y^2)^2+x^4+x^2y^2+y^2$

$=1+x^2(x^2+y^2)+y^2=1+x^2+y^2=1+1=2$