cho A là tập hợp các số tự nhiên có 10 chữ số được lấy từ tập M={0;1;2;3;4;5;6} ( các chữ số có thể giống nhau). Chọn ngẫu nhiên một số thuộc A, tính xác suất số được chọn chia hết cho 6
Những câu hỏi liên quan
Cho tập hợp A ={1;2;3;4;5}. Gọi B là tập số tự nhiên có 10 chữ số mà các chữ số lấy từ tập hợp A. Chọn ngẫu nhiên một số từ tập hợp B. Tính xác suất để số được chọn có một số lẻ chữ số 1 và một số chẵn chữ số 2.
"Một số lẻ chữ số 1 và 1 số chẵn chữ số 2" nghĩa là sao nhỉ?
Bạn có thể ghi 1 cách chính xác tuyệt đối đề bài không?
Đúng 1
Bình luận (0)
Tập các số tự nhiên chẵn từ số chẵn a đến số chẵn b có bao nhiêu phần tử?Tập hợp A gồm các số tự nhiên sao cho x + 5 12. Hỏi tập hợp A có bao nhiêu phần tử?Tập hợp B gồm các số tự nhiên sao cho x - 7 21. Hỏi tập hợp B có bao nhiêu phần tử?Tập hợp D gồm các số tự nhiên sao cho x . 0 10. Hỏi tập hợp D có bao nhiêu phần tử?Tập các số tự nhiên lẻ từ số lẻ a đến số lẻ b có bao nhiêu phần tử?Cho A là tập hợp các số có ba chữ số được tạo thành bởi ba chữ số 0 , 5 , 8 và mỗi chữ số chỉ xuất hiện một...
Đọc tiếp
Tập các số tự nhiên chẵn từ số chẵn a đến số chẵn b có bao nhiêu phần tử?
Tập hợp A gồm các số tự nhiên sao cho x + 5 = 12. Hỏi tập hợp A có bao nhiêu phần tử?
Tập hợp B gồm các số tự nhiên sao cho x - 7 = 21. Hỏi tập hợp B có bao nhiêu phần tử?
Tập hợp D gồm các số tự nhiên sao cho x . 0 = 10. Hỏi tập hợp D có bao nhiêu phần tử?
Tập các số tự nhiên lẻ từ số lẻ a đến số lẻ b có bao nhiêu phần tử?
Cho A là tập hợp các số có ba chữ số được tạo thành bởi ba chữ số 0 , 5 , 8 và mỗi chữ số chỉ xuất hiện một lần. Tập hợp A có bao nhiêu tập hợp con?
có 1 phần tử
A={7}có 1 phần tử
B là tập hợp rỗng
D là tập hợp rỗng
có 1 phần tử
tập hợp A có 4 tập hợp con
Đúng 0
Bình luận (0)
Gọi E là tập hợp các chữ số có hai chữ số khác nhau được lập từ tập hợp A{0; 1; 2; 3; 4; 5; 6}. Lấy ngẫu nhiên đồng thời hai phân tử trong E. Tính xác suất biến cố M “lấy được ít nhất một số chia hết cho 10”. A. P(M)
73
210
B. P(M)
61
210
C. P(M)
79
210
D. P(M)
13
42
Đọc tiếp
Gọi E là tập hợp các chữ số có hai chữ số khác nhau được lập từ tập hợp A={0; 1; 2; 3; 4; 5; 6}. Lấy ngẫu nhiên đồng thời hai phân tử trong E. Tính xác suất biến cố M = “lấy được ít nhất một số chia hết cho 10”.
A. P(M) = 73 210
B. P(M) = 61 210
C. P(M) = 79 210
D. P(M) = 13 42
Gọi M là tập hợp các số tự nhiên có ba chữ số lập được từ các chữ số 0,1,2,3,4,5,6,7 . Lấy ngẫu nhiên đồng thời 2 số từ tập M . Xác suất để cả 2 số lấy được đều có chữ số hàng chục nhỏ hơn các chữ số hàng trăm và hàng đơn vị là
1. Gọi S là tập hợp tất cả các số tự nhiên gồm 4 chữ số khác nhau được chọn từ các chữ số từ 1 đến 7 chọn ngẫu nhiên 1 số từ S tính xác suất để số được chọn là số lẻ và có mặt chữ số 5.2. Tập hợp E gồm các chữ số từ 1 đến 5. Gọi M là tập hợp tatts cả các số tự nhiên có ít nhất 3 chữ số đôi 1 khác nhau. Lấy 1 số từ M tính xác suất để tổng các chữ số của số đó bằng 10.3. Từ các chữ số 0,1,2,3,4,5,6,7 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhautrong đó có đúng 2 chữ số chẵn
Đọc tiếp
1. Gọi S là tập hợp tất cả các số tự nhiên gồm 4 chữ số khác nhau được chọn từ các chữ số từ 1 đến 7 chọn ngẫu nhiên 1 số từ S tính xác suất để số được chọn là số lẻ và có mặt chữ số 5.
2. Tập hợp E gồm các chữ số từ 1 đến 5. Gọi M là tập hợp tatts cả các số tự nhiên có ít nhất 3 chữ số đôi 1 khác nhau. Lấy 1 số từ M tính xác suất để tổng các chữ số của số đó bằng 10.
3. Từ các chữ số 0,1,2,3,4,5,6,7 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhautrong đó có đúng 2 chữ số chẵn
Cho tập hợp C={0;3;6}.
a) Viết tất cả các số tự nhiên lẻ có 4 chữ số mà các chữ số của nó lấy ra từ tập hợp C.
b) Viết tất cả các số tự nhiên có 4 chữ số mà các chữ số của nó lấy ra từ tập hợp C và chữ số 6 có giá trị là 600.
c) Viết tất cả các số tự nhiên chẵn có 3 chữ số mà các chữ số của nó lấy ra tự C.
Xem chi tiết
a) H = { 3003; 3033; 3333; 6003; ....; 6663 }
b) Y = { 3000; 3003; 3006;.....; 6666 }
c) G = { 300; 306; 330; 336;....; 666 }
Gọi E là tập hợp các chữ số có hai chữ số khác nhau được lập từ tập hợp A{0;1;2;3;4;5;6}. Lấy ngẫu nhiên đồng thời hai phân tử trong E. Tính xác suất biến cố M “lấy được ít nhất một số chia hết cho 10”. A. B. C. D.
Đọc tiếp
Gọi E là tập hợp các chữ số có hai chữ số khác nhau được lập từ tập hợp A={0;1;2;3;4;5;6}. Lấy ngẫu nhiên đồng thời hai phân tử trong E. Tính xác suất biến cố M = “lấy được ít nhất một số chia hết cho 10”.
A. 
B. 
C. 
D. 
Đáp án D
Số phần tử của E là 
Trong E có 6 số chia hết cho 10 là 10, 20, 30, 40, 50, 60.
Số cách lấy ngẫu nhiên đồng thời hai phần tử trong E là 
cặp.
Biến cố M “lấy được ít nhất một số chia hết cho 10” gồm 
cách lấy được 2 số chia hết cho 10 và 
cách lấy được 1 số chia hết cho 10 và 1 số không chia hết cho 10.
Vậy số phần tử của biến cố M là
Đúng 0
Bình luận (0)
Từ tập hợp tất cả các số tự nhiên có năm chữ số mà các chữ số đều khác 0, lấy ngẫu nhiên một số. Xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là:
A
.
504
59049
B
.
7560
59049
C
.
1260
59049
D
.
12600...
Đọc tiếp
Từ tập hợp tất cả các số tự nhiên có năm chữ số mà các chữ số đều khác 0, lấy ngẫu nhiên một số. Xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là:
A . 504 59049
B . 7560 59049
C . 1260 59049
D . 12600 59049
Chọn D
Không gian mẫu được mô tả là Ω : “Các số tự nhiên có 5 chữ số khác 0”.
Số phần tử của không gian mẫu là: 
Gọi biến cố A: “Các số tự nhiên có 5 chữ số khác 0 trong đó chỉ có mặt ba chữ số khác nhau”.
Số cách chọn 3 chữ số phân biệt a, b, c từ 9 chữ số tự nhiên khác 0 là C 9 3 . Chọn 2 chữ số còn lại từ 3 chữ số đó, có 2 trường hợp sau:
TH1: Nếu cả 2 chữ số còn lại cùng bằng 1 trong 3 số a, b, c thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị của 5 chữ số chẳng hạn a, a, a , b, c tạo ra một số tự nhiên; nhưng cứ hoán vị của các vị trí mà a, a, a chiếm chỗ thì chỉ tạo ra cùng 1 số tự nhiên. Do đó, trong TH1 có tất cả 3 . 5 ! 5 số tự nhiên.
TH2: 1 trong 2 chữ số còn lại bằng 1 trong 3 chữ số và chữ số kia bằng một chữ số a, b, c khác trong 3 chữ số đó thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị chẳng hạn a, a, b, b, c tạo ra một số tự nhiên nhưng cứ 2! cách hoán vị a và 2! cách hoàn vị b mà vẫn cho ra cùng 1 số. Do đó, trong TH2 có tất cả: 3 . 5 ! 2 ! . 2 ! số tự nhiên.
Suy ra số phần tử của biến cố A là: 
Vậy xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là: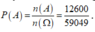 
Đúng 0
Bình luận (0)
Cho tập hợp X{0;1;2;3;4;5;6;7;8;9}, người ta lập 2 tập hợp con của X, tập hợp A{0;1;2;...;n} gồm n+1 số tự nhiên đầu tiên và B{n+1;n+2;...;2n}. Từ mỗi tập hợp A và B đó, người ta lập số tự nhiên có 5 chữ số đôi một khác nhau, trong số đó có hai chữ số hàng chục nghìn và hàng nghìn được viết bởi các chữ số lấy trong tập hợp A, 3 chữ số còn lại được lấy trong tập hợp B. Hỏi lập được bao nhiêu số tự nhiên như vậy và số lớn nhất là bao nhiêu?
Đọc tiếp
Cho tập hợp X={0;1;2;3;4;5;6;7;8;9}, người ta lập 2 tập hợp con của X, tập hợp A={0;1;2;...;n} gồm n+1 số tự nhiên đầu tiên và B={n+1;n+2;...;2n}. Từ mỗi tập hợp A và B đó, người ta lập số tự nhiên có 5 chữ số đôi một khác nhau, trong số đó có hai chữ số hàng chục nghìn và hàng nghìn được viết bởi các chữ số lấy trong tập hợp A, 3 chữ số còn lại được lấy trong tập hợp B. Hỏi lập được bao nhiêu số tự nhiên như vậy và số lớn nhất là bao nhiêu?