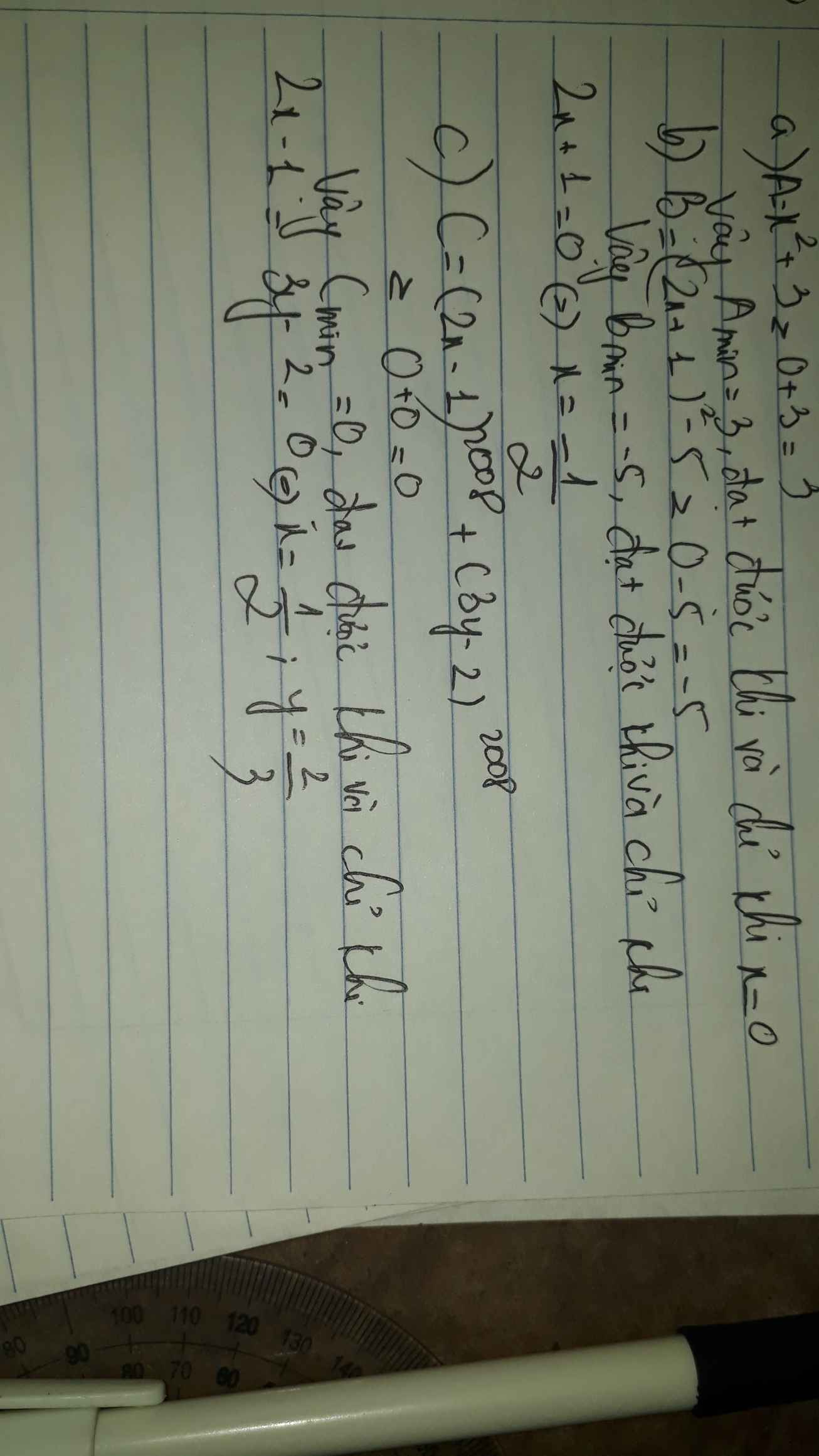Tính giá trị biểu thức A=2008/3 + 2008/15 + 2008/35 +2008/63 + .........+2008/4032063
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6

Những câu hỏi liên quan
\(\sqrt{2008+\sqrt{2008+\sqrt{2008+...+\sqrt{2008}}}}\)
Trong biểu thức trên, số 2008 xuất hiện 2008 lần. Tính giá trị của biểu thức.
BÀI 1 : TÍNH GIÁ TRỊ BIỂU THỨC
a) A = 5 / 0,(2008) +5 / 0,0(2008) + 5/ 0,00(2008)
Cho x=2009 . Tính giá trị của biểu thức : A=x2009 - 2008.x2008 - 2008.x2007 - ... - 2008x + 1
x=2009 => 2008 = x-1
Thay x=2009 và 2008 = x -1 vào A:
\(A=x^{2009}-\left(x-1\right)\cdot x^{2008}-\left(x-1\right)\cdot x^{2007}-...-\left(x-1\right)\cdot x+1\)
\(=x^{2009}-x^{2009}+x^{2008}-x^{2008}+.....-x^2+x+1\)
\(=x+1=2009+1=2010\)
Đúng 0
Bình luận (0)
Cho đa thức \(f\left(x\right)=x^{17}-2008\times x^{16}+2008\times x^{15}-2008\times x^{14}+...-2008\times x\)Tính giá trị đa thức khi x= 2007
Tính giá trị biểu thức E = \(\sqrt{1+2007^2+\dfrac{2007^2}{2008^2}}+\dfrac{2007}{2008}\)
Trước tiên ta cần chứng minh : \(1^2+n^2+\dfrac{n^2}{\left(n+1\right)^2}\text{=}\left(n+1-\dfrac{n}{n+1}\right)^2\)
\(\Leftrightarrow2.\left(\dfrac{n\left(n+1\right)}{n+1}-\dfrac{n}{n+1}-\dfrac{n^2}{n+1}\right)\text{=}0\)
\(\Leftrightarrow2.0\text{=}0\left(LĐ\right)\)
Ta có : \(E\text{=}\sqrt{1+2007^2+\dfrac{2007^2}{2008^2}}+\dfrac{2007}{2008}\)
Với bổ đề trên thì :
\(E\text{=}\sqrt{\left(2007+1-\dfrac{2007}{2008}\right)^2}+\dfrac{2007}{2008}\)
\(E\text{=}2008+\dfrac{2007}{2008}-\dfrac{2007}{2008}\)
\(E\text{=}2008\)
Đúng 1
Bình luận (0)
Giá trị biểu thức A =
2008+2007/2+2006/3+2005/4+...+2/2007+1/2008
1/2+1/3+1/4+1/5+...+1/2008+1/2009
Tìm A
Xem thêm câu trả lời
Cho 2008 số thỏa mãn a1 + a2 + .... + a2008 khác 0 và \(\frac{a_1}{a_2}=\frac{a_2}{a_3}=...=\frac{a_{2007}}{a_{2008}}=\frac{a_{2008}}{a_1}\)
Hãy tính giá trị của biểu thức: N = \(\frac{a_1^2+a_2^2+.....+a^2_{2007}+a^2_{2008}}{\left(a_1+a_2+.....+a_{2007}+a_{2008}\right)^2}\)
GIÚP MÌNH VỚI
Ta có
\(\frac{a_1}{a_2}+\frac{a_2}{a_3}+...+\frac{a_{2008}}{a_1}=\frac{a_1+...+a_{12}+...+a_{2008}}{a_2+a_3+...+a_1}=1\)
Từ đó a1 = a2 = a3 = ... = a2008
\(\Rightarrow N=\frac{a^2_1+a^2_2+...+a_{2008}^2}{\left(a_1+a_2+...+a_{2008}\right)^2}=\frac{2008a^2_1}{\left(2008a_1\right)^2}=\frac{1}{2008}\)
Đúng 0
Bình luận (0)
alibaba mình nghĩ là thay dấu + là dấu = sẽ đúng hơn
Đúng 0
Bình luận (0)
Ừ. Bấm nhầm dấu thôi. Nhưng mình nghĩ bạn đó sẽ đọc được nên để vậy luôn
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của các biểu thức sau:
a) A = x\(^2\) + 3
b) B = (2x + 1)\(^2\) - 5
c) C = (2x - 1)\(^{2008}\) + (3y - 2)\(^{2008}\)
a)Ta có: \(x^2\ge0\Rightarrow x^2+3\ge3\)
Dấu "=" xảy ra \(\Leftrightarrow x=0\)
Vậy \(A_{Min}=3 khi x=0\)
b) \(\left(2x+1\right)^2\ge0\Rightarrow\left(2x+1\right)^2-5\ge-5\)
Dấu "=" xảy ra \(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy \(B_{Min}=-5khix=-\dfrac{1}{2}\)
c) \(\left(2x-1\right)^{2008}\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow x=\dfrac{1}{2}\)
\(\left(3y-2\right)^{2008}\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow y=\dfrac{2}{3}\)
\(\Rightarrow\left(2x-1\right)^{2008}+\left(3y-2\right)^{2008}\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{2}{3}\end{matrix}\right.\)
Vậy \(C_{Min}=0khix=\dfrac{1}{2}vày=\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
A=|x-2008| + |x-2009| + |y-2010| +|2011| +2008
tìm giá trị nhỏ nhất của biểu thức trên