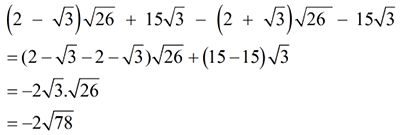Truc can thuc o mau: \(\frac{1}{2+\sqrt{3}-\sqrt{6}}\)

Những câu hỏi liên quan
truc can thuc o mau
\(\dfrac{26}{2\sqrt{3}+5}\)
\(\dfrac{26}{2\sqrt{3}+5}=\dfrac{26\left(2\sqrt{3}-5\right)}{\left(2\sqrt{3}\right)^2-5^2}=\dfrac{26\left(2\sqrt{3}-5\right)}{-13}=-2\left(2\sqrt{3}-5\right)=10-4\sqrt{3}\)
Đúng 0
Bình luận (0)
truc can thuc va tinh
a) \(\frac{5}{4-\sqrt{11}}+\frac{1}{3+\sqrt{7}}-\frac{6}{\sqrt{7}-2}-\frac{\sqrt{7}-5}{2}\)
b) \(\frac{4}{\sqrt{5}-\sqrt{2}}+\frac{3}{\sqrt{5}-2}-\frac{2}{\sqrt{3}-2}+\frac{\sqrt{3}-1}{6}\)
Bạn xem hộ mk đề cậu b nhé căn 5- căn 2 hay là căn 5 - 2
Đúng 0
Bình luận (1)
Chung minh cac dang thuc sau\(\left(\frac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\frac{\sqrt{216}}{3}\right).\frac{1}{\sqrt{6}}=-1,5\)
https://www.youtube.com/watch?v=ylWDD1Df-e8
Bạn tham khảo ở đây nha! ( bài này ở 7:50 nha)
Học tốt!
Đúng 0
Bình luận (0)
Rut gon bieu thuc
1)\(\frac{\sqrt{6-2\sqrt{5}}}{2-2\sqrt{5}}\)
2)\(\frac{\sqrt{7-4\sqrt{3}}}{1-\sqrt{3}}\)
1) \(\frac{\sqrt{6-2\sqrt{5}}}{2-2\sqrt{5}}=\frac{\sqrt{\left(\sqrt{5}-1\right)^2}}{2\left(1-\sqrt{5}\right)}=\frac{\sqrt{5}-1}{2\left(1-\sqrt{5}\right)}=-\frac{1}{2}\)
2) \(\frac{\sqrt{7-4\sqrt{3}}}{1-\sqrt{3}}=\frac{\sqrt{\left(2-\sqrt{3}\right)^2}}{1-\sqrt{3}}=\frac{2-\sqrt{3}}{1-\sqrt{3}}\)
Đúng 0
Bình luận (0)
trục can thuc A= \(\frac{4}{3+\sqrt{5}+\sqrt{2+2\sqrt{5}}}\)
B=\(\frac{2}{\sqrt[3]{4}+\sqrt[3]{2}+2}\)
C=\(\frac{2}{2\sqrt[3]{2}+2+\sqrt[3]{4}}\)
1/ Rut gon bieu thuc sau:
a) \(\sqrt{12-2\sqrt{35}}+\sqrt{7-2\sqrt{10}}-\sqrt{\sqrt{49}}\)
b) \(\frac{\sqrt{7}-5}{2}-\frac{6}{\sqrt{7}-2}+\frac{1}{3+\sqrt{7}}+\frac{3}{5+2\sqrt{7}}\)
Rut gon bieu thuc:
a) (2-\(\sqrt{3}\))\(\sqrt{26+15\sqrt{3}}-\left(2+\sqrt{3}\right)\sqrt{26-15\sqrt{3}}\)
b) \(\frac{1}{\sqrt{3}}+\frac{1}{3\sqrt{2}}+\frac{1}{\sqrt{3}}\sqrt{\frac{5}{12}-\frac{1}{\sqrt{6}}}\)
c) \(\frac{\sqrt{7+\sqrt{5}}+\sqrt{7-\sqrt{5}}}{\sqrt{7+2\sqrt{11}}}-\sqrt{3-2\sqrt{2}}\)
Thuc hien phep tinh \(\frac{5}{4-\sqrt{11}}+\frac{1}{3+\sqrt{7}}-\frac{6}{\sqrt{7}-2}-\frac{\sqrt{7}-5}{2}\)
Cho bieu thuc:
P=\(\frac{1}{\sqrt{x}+2}-\frac{5}{x-\sqrt{x}-6}-\frac{\sqrt{x}-2}{3-\sqrt{x}}\)
a. Rut gon bieu thuc P
b.Tim GTLN cua P sau khi rut gon
đk: x>=0; x khác 3
a) \(P=\frac{\sqrt{x}-3}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)}-\frac{5}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)}+\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}-3}=\frac{\sqrt{x}-3-5+x-4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)}=\frac{x+\sqrt{x}-12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)}\)
\(P=\frac{\left(\sqrt{x}+4\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)}=\frac{\sqrt{x}+4}{\sqrt{x}+2}\)
b) \(P=\frac{\sqrt{x}+2+2}{\sqrt{x}+2}=1+\frac{2}{\sqrt{x}+2}\)
ta có: \(x\ge0\Rightarrow\sqrt{x}\ge0\Leftrightarrow\sqrt{x}+2\ge2\Leftrightarrow\frac{2}{\sqrt{x}+2}\le1\Leftrightarrow1+\frac{2}{\sqrt{x}+2}\le2\Rightarrow MaxP=2\Rightarrow x=0\)
Đúng 0
Bình luận (0)
Cho bieu thuc: \(p=\left(\frac{1}{\sqrt{x}-\sqrt{x-1}}-\frac{x-3}{\sqrt{x-1}-\sqrt{2}}\right)\left(\frac{2}{\sqrt{2}-\sqrt{x}}-\frac{\sqrt{x}+\sqrt{2}}{\sqrt{2x}-x}\right)\)
a) Tim DKXD cua bieu thuc p
b) Rut gon bieu thuc p