Thế nào là sai số tuyệt đối ứng với lần đo

Những câu hỏi liên quan
Bảng 3.4 thể hiện kết quả đo khối lượng của một túi trái cây bằng cân đồng hồ. Em hãy xác định sai số tuyệt đối ứng với từng lần đo, sai số tương đối của phép đo. Biết sai số dụng cụ là 0,1 kg.Sai số tuyệt đối của phép đo: Δm¯¯¯¯¯¯¯¯¯Δm+Δmdc?Δ�Δ�¯+Δ���?Sai số tương đối của phép đo: δmΔm¯¯¯¯¯m.100%?��Δ��¯.100%?Kết quả phép đo: m¯¯¯¯¯m±Δm?
Đọc tiếp
Bảng 3.4 thể hiện kết quả đo khối lượng của một túi trái cây bằng cân đồng hồ. Em hãy xác định sai số tuyệt đối ứng với từng lần đo, sai số tương đối của phép đo. Biết sai số dụng cụ là 0,1 kg.
Sai số tuyệt đối của phép đo:
Sai số tương đối của phép đo:
Kết quả phép đo:
Bảng 3.4 thể hiện kết quả đo khối lượng của một túi trái cây bằng cân đồng hồ. Em hãy xác định sai số tuyệt đối ứng với từng lần đo, sai số tương đối của phép đo. Biết sai số dụng cụ là 0,1 kg.Sai số tuyệt đối của phép đo: Delta m overline {Delta m} + Delta {m_{dc}} ?Sai số tương đối của phép đo: delta m frac{{Delta m}}{{overline m }}.100% ?Kết quả phép đo: m overline m pm Delta m ?
Đọc tiếp
Bảng 3.4 thể hiện kết quả đo khối lượng của một túi trái cây bằng cân đồng hồ. Em hãy xác định sai số tuyệt đối ứng với từng lần đo, sai số tương đối của phép đo. Biết sai số dụng cụ là 0,1 kg.
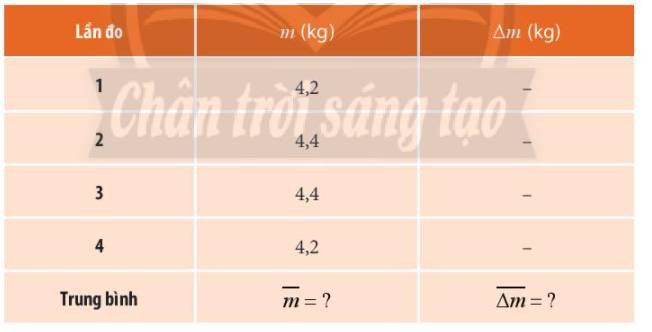
Sai số tuyệt đối của phép đo: \(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = ?\)
Sai số tương đối của phép đo: \(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = ?\)
Kết quả phép đo: \(m = \overline m \pm \Delta m = ?\)
Giá trị trung bình khối lượng của túi trái cây là:
\(\overline m = \frac{{{m_1} + {m_2} + {m_3} + {m_4}}}{4} = \frac{{4,2 + 4,4 + 4,4 + 4,2}}{4} = 4,3(kg)\)
Sai số tuyệt đối ứng với mỗi lần đo là:
\(\begin{array}{l}\Delta {m_1} = \left| {\overline m - {m_1}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\\\Delta {m_2} = \left| {\overline m - {m_2}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_3} = \left| {\overline m - {m_3}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_4} = \left| {\overline m - {m_4}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\end{array}\)
Sai số tuyệt đối trung bình của phép đo:
\(\overline {\Delta m} = \frac{{\Delta {m_1} + \Delta {m_2} + \Delta {m_3} + \Delta {m_4}}}{4} = \frac{{0,1 + 0,1 + 0,1 + 0,1}}{4} = 0,1(kg)\)
Sai số tuyệt đối của phép đo là:
\(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = 0,1 + 0,1 = 0,2(kg)\)
Sai số tương đối của phép đo là:
\(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = \frac{{0,2}}{{4,2}}.100\% = 4,65\% \)
Kết quả phép đo:
\(m = \overline m \pm \Delta m = 4,3 \pm 0,2(kg)\)
Đúng 0
Bình luận (0)
Câu 1 .Đo chiều dài một quyển sổ 5 lần được kết quả là: 200,1mm; 200mm; 199mm; 200,05mm; 199,05mm. độ chia nhỏ nhất trên thước đo là 1mm.
a. Tính sai số tuyệt đối và sai số tỷ đối của phép đo?
b. Viết kết quả phép đo?
a. Sai số tuyệt đối và sai số tỷ đối:
Ta tính tổng độ sai số của các giá trị đo lượng thực như sau:
Sai sốĐộ sai số
| 0 | 200mm |
| 0 | 200mm |
| 1 | 199mm |
| 5 | 200,05mm |
| 1 | 199,05mm |
Tổng độ sai số = 0 + 0 + 1 + 5 + 1 = 7
Giá trị thực là 550mm, vậy sai số tuyệt đối = |550 - 500| = 100.
Tỷ đối sai số = (7/1000) x 100 = 0.7%.
b. Kết quả phép đo:
Sai số tuyệt đối: 100mmSai số tỷ đối: 0.7%Vậy kết quả phép đo của chiều dài quyển sổ là 550mm với sai số tuyệt đối là 100mm và sai số tỷ đối là 0.7%.
Đúng 0
Bình luận (0)
1 Đo chiều dài một quyển sổ 5 lần được kết quả là: 200,1mm; 200mm; 199mm; 200,05mm; 199,05mm. độ chia nhỏ nhất trên thước đo là 1mm. a. Tính sai số tuyệt đối và sai số tỷ đối của phép đo? b. Viết kết quả phép đo
Xem chi tiết
a. Sai số tuyệt đối (MAD) và sai số tỷ đối (MAPE) được tính như sau:
Phép đo thực tế (TTT): 200,1mm, 200mm, 199mm, 200,05mm, 199,05mm
Phép đo lý thuyết (TDT): 200mm, 200mm, 200mm, 200mm, 200mm, 200mm
MAD = |(TTT - TDT)| = |(200,1 - 200), (200 - 200), (199 - 200), (200,05 - 200), (199,05 - 200)| = (0,1), 0, 1, 0, 1, 1 mm
MAPE = |(TTT - TDT)/TTT)|*100 = |(200,1 - 200)/200,1), (200 - 200)/200), (199 - 200)/199), (200,05 - 200)/200,05), (199,05 - 200)/199,05)|*100 = 0,05%, 0%, 0,05%, 0,05%, 0,05%
b. Kết quả phép đo:
Độ lỗi tuyệt đối tối đa: 1,1 mm (từ 0,1 mm tới 1,1 mm)Độ lỗi tỷ đối tối đa: 0,05% (từ 0% tới 0,05%)Vậy độ lỗi tuyệt đối và tỷ đối tối đa của phép đo đo chiều dài quyển sách 5 lần là:
Độ lỗi tuyệt đối tối đa: 1,1 mmĐộ lỗi tỷ đối tối đa: 0,05%
Đúng 0
Bình luận (0)
cho bảng số liệu kết quả đo của 1 bịch trái cây. Hãy hoàn thành bảng số liệu và tính sai số tuyệt đối của phép đo, sai số trương đối của phép đo và viết giá trị của phép đo kèm theo sai số. Biết sai số dụng cụ là 0,1 kg lần đo m(kg)Δm(kg)13,2 23,4 33,4 43,2 biểu diễn kết quả đo
Đọc tiếp
cho bảng số liệu kết quả đo của 1 bịch trái cây. Hãy hoàn thành bảng số liệu và tính sai số tuyệt đối của phép đo, sai số trương đối của phép đo và viết giá trị của phép đo kèm theo sai số. Biết sai số dụng cụ là 0,1 kg
| lần đo | m(kg) | Δm(kg) |
| 1 | 3,2 | |
| 2 | 3,4 | |
| 3 | 3,4 | |
| 4 | 3,2 | |
biểu diễn kết quả đo
xử lý số liệu phép đo của bài toán sau đây một bạn dùng thước dài có độ chia nhỏ nhất bằng 1 mm để đo chiều dài của một tấm vải kết quả đo được 5 lần đo theo thứ tự 50 52 51 51 50 (cm)
a,hãy tính giá trị trung bình của l
b,tính sai số tuyệt đối của mỗi lần đo
c ,tính sai số tuyệt đối trung bình của 5 lần đo
d,sai số tuyệt đối của phép đo e,sai số tỉ đối của phép đo
Đọc tiếp
xử lý số liệu phép đo của bài toán sau đây một bạn dùng thước dài có độ chia nhỏ nhất bằng 1 mm để đo chiều dài của một tấm vải kết quả đo được 5 lần đo theo thứ tự 50 52 51 51 50 (cm)
a,hãy tính giá trị trung bình của l
b,tính sai số tuyệt đối của mỗi lần đo
c ,tính sai số tuyệt đối trung bình của 5 lần đo
d,sai số tuyệt đối của phép đo e,sai số tỉ đối của phép đo
a) Nhờ bạn bấm máy tính kiểm tra nhé.
Giá trị trung bình của l:
\(\overline{l}=\frac{l_1+l_2+..+l_n}{n}=\frac{50+52+51+51+50}{5}=50,8\)
b) Sai số tuyệt đối \(\Delta A_1=\left|\overline{A}-A_1\right|;\Delta A_2=\left|\overline{A}-A_2\right|\)
Khi đó sai số tuyệt đối ở mỗi lần đo là
\(\Delta l_1=\left|\overline{I}-I_1\right|=\left|50,8-50\right|=0,8.\)
Tương tự cho 4 lần đo tiếp theo.
c) Sai số tuyệt đối trung bình
\(\overline{\Delta I}=\frac{\Delta I_1+\Delta I_2+..+\Delta I_5}{5}=...\)
d) Sai số tuyệt đối của phép đo \(\Delta l=\overline{\Delta l}+\Delta l'=\overline{\Delta l}+\frac{1}{2}\)số chia nhỏ nhât = ....
e) Sai số tỉ đối \(\delta l=\frac{\Delta l}{\overline{l}}.100\%\)
Đúng 0
Bình luận (0)
Thế nào là sai số tuyệt đối của một số gần đúng? Thế nào là độ chính xác của một số gần đúng?
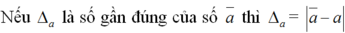
được gọi là sai số tuyệt đối của số gần đúng a.
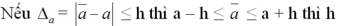
được gọi là độ chính xác của số gần đúng a.
Đúng 0
Bình luận (0)
giúp mình với ạ!!!
câu 1: vôn kế thang đo 500V , cấp chính xác 1,2 thì sai số tuyệt đối lớn nhất là
A. 0,06
B. 0,6
C. 6
D. 60
câu 2: ampe kế thanh đo 50A , cấp chính xác 1,2 thì sai số tuyệt đối lớn nhất là ?
A. 0,06
B.0,6
C.6
D.60
cậu học trường thcs bình chuẩn lớp 9a8 à((:?
Đúng 0
Bình luận (2)
1 d.60
2 b.0,6
trả lời câu nãy giùm:))
Đúng 0
Bình luận (1)
một học sinh dùng thước cặp có sai số dụng cụ 0.01mm để đo đường kính d của 1 viên bi, giá trị trung bình của n lần đo đường kính là \(\overline{d}\)=12mm và sai số tuyệt đối trung bình của n lần đo là \(\overline{\Delta d}\)=0.05mm. kết quả phép đo là


















