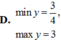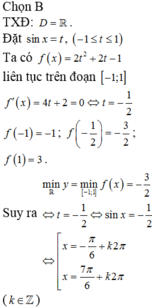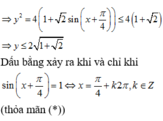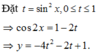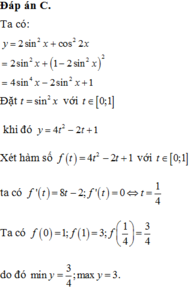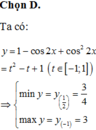Tìm giá trị lớn nhất nhỏ nhất của y=2sinx+2cosx-2sin2x

Những câu hỏi liên quan
Tìm giá trị nhỏ nhất của hàm số
y
2
sin
2
x
+
2
sin
x
-
1
A.
-
2
3
B.
-
3
2
C. 1 D.
1
2
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = 2 sin 2 x + 2 sin x - 1
A. - 2 3
B. - 3 2
C. 1
D. 1 2
Tìm giá trị lớn nhất của hàm số
y
1
+
2
cos
x
+
1
+
2
sin
x
A. B. C. D.
Đọc tiếp
Tìm giá trị lớn nhất của hàm số y = 1 + 2 cos x + 1 + 2 sin x
A.![]()
B. ![]()
C.![]()
D. ![]()
Đáp án B
Điều kiện 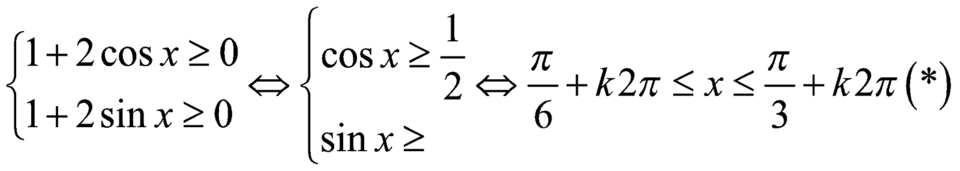
Theo bất đẳng thức BunhiaCopxki: ![]()
![]()
Dấu bằng xảy ra khi và chỉ khi ![]() (thỏa mãn (*))
(thỏa mãn (*))
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất của hàm số
y
1
+
2
cos
x
+
1
+
2
sin
x
A.
4
1
+
2
B.
2
1
+
2
C.
2
2
D. ...
Đọc tiếp
Tìm giá trị lớn nhất của hàm số y = 1 + 2 cos x + 1 + 2 sin x
A. 4 1 + 2
B. 2 1 + 2
C. 2 2
D. 2
Tìm giá trị lớn nhất M của hàm số y = 2 sin x - 2 cos x - 5
A. M = 9
B. M = 2 2 - 5
C. M = 7
D. M = - 2 2 - 5
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y
2
sin
2
x
+
cos
2
2
x
A. B. C. D.
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 2 sin 2 x + cos 2 2 x
A.![]()
B. ![]()
C. ![]()
D. ![]()
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y
2
sin
2
x
+
cos
2
2
x
A.
m
a
x
y
3
2
,
m
i
n
y
1
2
B.
m
a
x
y...
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 2 sin 2 x + cos 2 2 x
A. m a x y = 3 2 , m i n y = 1 2
B. m a x y = 3 , m i n y = - 1 2
C. m a x y = 1 2 , m i n y = - 1 2
D. m a x y = 3 , m i n y = 3 4
Tìm giá trị nhỏ nhất , giá trị lớn nhất của :
y = \(\sqrt{3}\)sin2x + 2sin2x -1
\(y=\sqrt{3}sin2x-cos2x=2\left(\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x\right)=2sin\left(2x-\dfrac{\pi}{6}\right)\)
Do \(-1\le sin\left(2x-\dfrac{\pi}{6}\right)\le1\Rightarrow-2\le y\le2\)
\(y_{max}=2\) khi \(sin\left(2x-\dfrac{\pi}{6}\right)=1\)
\(y_{min}=-2\) khi \(sin\left(2x-\dfrac{\pi}{6}\right)=-1\)
Đúng 1
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau:
y
2
sin
2
x
+
cos
2
2
x
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau: y = 2 sin 2 x + cos 2 2 x
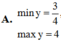
![]()
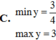
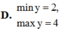
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau:
y
2
sin
2
x
+
cos
2
2
x
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau: y = 2 sin 2 x + cos 2 2 x
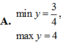
![]()
![]()