tính các góc tứ giác EFGH
biết E:G:H:F = 1:2:4:5
Bài 2: Cho tứ giác EFGH biết E:F:G:H = 1: 2: 4:5 .Tính các góc của tứ giác
Tứ giác \(EFGH\) có các góc cho như trong Hình 5.
a) Chứng minh rằng \(EFGH\) là hình thang
b) Tìm góc chưa biết của tứ giác
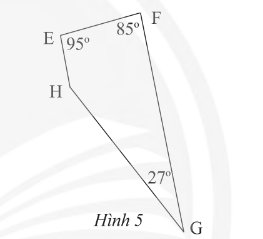
a) Ta có:
\(\widehat {\rm{E}} + \widehat {\rm{F}} = 95^\circ + 85^\circ = 180^\circ \)
Mà hai góc ở vị trí Trong cùng phía
Suy ra \(EH\;{\rm{//}}\;FG\)
Suy ra: \(EFGH\) là hình thang
b) Xét hình thang \(EFGH\) ta có: \(\widehat E + \widehat F + \widehat G + \widehat H = 360^\circ \)
\(\begin{array}{l}95^\circ + 85^\circ + 27^\circ + \widehat H = 360^\circ \\\widehat H = 153^\circ \end{array}\)
a) Xét ΔABC có
E là trung điểm của AB(gt)
F là trung điểm của BC(gt)
Do đó: EF là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒EF//AC và \(EF=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔADC có
H là trung điểm của AD(gt)
G là trung điểm của CD(gt)
Do đó: HG là đường trung bình của ΔADC(Định nghĩa đường trung bình của tam giác)
⇒HG//AC và \(HG=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra HG//EF và HG=EF
Xét ΔABD có
E là trung điểm của AB(gt)
H là trung điểm của AD(gt)
Do đó: EH là đường trung bình của ΔABD(Định nghĩa đường trung bình của tam giác)
⇒EH//BD và \(EH=\dfrac{BD}{2}\)(Định lí 2 về đường trung bình của tam giác)
Ta có: EH//BD(cmt)
BD⊥AC(gt)
Do đó: EH⊥AC(Định lí 2 từ vuông góc tới song song)
Ta có: HG//AC(cmt)
EH⊥AC(Cmt)
Do đó: HG⊥HE(Định lí 2 từ vuông góc tới song song)
hay \(\widehat{EHG}=90^0\)
Xét tứ giác EHGF có
HG//EF(cmt)
HG=FE(cmt)
Do đó: EHGF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành EHGF có \(\widehat{EHG}=90^0\)(cmt)
nên EHGF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Ta có: EFGH là hình chữ nhật(cmt)
nên \(S_{EFGH}=EF\cdot EH\)
\(\Leftrightarrow S_{EFGH}=\dfrac{AC}{2}\cdot\dfrac{BD}{2}=\dfrac{10}{2}\cdot\dfrac{8}{2}=5\cdot4=20cm^2\)
Vậy: Diện tích tứ giác EFGH khi AC=10cm và BD=8cm là 20cm2
c) Hình chữ nhật EFGH trở thành hình vuông khi EH=HG
hay AC=BD
Vậy: Khi tứ giác ABCD có thêm điều kiện AC=BD thì EFGH trở thành hình vuông
Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi E , F, G, H lần lượt là các trung điểm của các cạnh AB, BC, CD, DA.
a) Tứ giác EFGH là hình gì.
b) Biết Ac = 10cm, BD = 8cm. Tính diện tích tứ giác EFGH.
c) Cần có điều kiện gì để tứ giác EFGH là hình vuông
Cho hình bình hành ABCD, AB = 6cm, AD = 4cm. Các tia phân giác của các góc A, B, C, D cắt nhau tạo thành tứ giác EFGH.
a) Tứ giác EFGH là hình gì ?
b ) Tính độ dài đường chéo của tứ giác EFGH
c ) Hinh bình hành ABCD có thêm điều kiện gì để diện tích tứ giác EFGH lớn nhất ?
Bài 1: Cho tứ giác ABCD và các điểm M,N,P,Q theo thứ tự là trung điểm của AB, BC, CD,DA
a. Chứng minh rằng: TỨ giác MNPQ là hình bình hành
b. 2 đường chéo AC và BD phải có điều kiện gì thì MNPQ là hình thoi, hình vuông, hình chữ nhật.
Bài 2: Cho tứ giác ABCD biết AC vuông góc với BD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA
a. Tứ giác EFGH là hình gì? Vì sao?
b. Tính diện tích tứ giác EFGH biết AC=6cm ; BD = 4 cm
Help me!
cho tứ giác ABCD biết ac vuông góc với bd . gọi E,F,G,H theo thứ tự là trung điểm của AB,BC,CD,DA
a) tú giác EFGH là hình gì ? vì sao?
b) tính diện tích của tứ giác EFGH , biết AC=6CM,BD=4CM
a: Xét ΔABD có
E là trung điểm của AB
H là trung điểm của AD
Do đó: EH là đường trung bình
=>EH//BD và EH=BD/2(1)
Xét ΔBCD có
F là tđiểm của BC
G là tđiểm của CD
Do đó: FG là đường trung bình
=>FG//BD và FG=BD/2(2)
Xét ΔADC có
H là tđiểm của AD
G là tđiểm của CD
Do đó: GH là đường trung bình
=>GH⊥EH(3)
Từ (1), (2) và (3) suy ra EFGH là hình chữ nhật
Cho hình thang cân ABCD,đáy CD.E,F,G,H thứ tự là trung điểm của AB,BD,CD,AC
a)Cmr: EG là phân giác góc FEH
b)Tính các góc của tứ giác EFGH biết góc BCD=55 độ
a: Xét ΔABC có
E là trung điểm của AB
H là trung điểm của AC
Do đó: EH là đường trung bình của ΔABC
Suy ra: EH//BC và EH=BC/2(1)
Xét ΔBDC có
F là trung điểm của BD
G là trung điểm của CD
Do đó: FG là đường trung bình của ΔBDC
Suy ra: FG//BC và FG=BC/2(2)
Xét ΔABD có
E là trung điểm của AB
F là trung điểm của BD
Do đó: EF là đường trung bình của ΔABD
Suy ra: EF//AD và EF=AD/2
hay EF=BC/2(3)
Từ (1) và (2) suy ra EH//FG và EH=FG
Từ (2) và (3) suy ra EF=FG
Xét tứ giác EHGF có
EH//FG
EH=FG
Do đó: EHGF là hình bình hành
mà EF=FG
nên EHGF là hình thoi
1/ Cho tam giác ABC. Qua điểm D thuộc BC. Vẽ các đường thẳng song song với AB, AC tạo thành 1 hình bình hành có diện tích bằng(3/8) diện tích tam giác ABC. tính tỉ số BD/BC
2/ Hình vuông EFGH. Nội tiếp hình vuông ABCD sao cho EFGH chia các cạnh của hình vuông theo tỉ số k. Tính k. Biết rằng diện tích EFGH=(5/9) diện tích ABCD
3/ Tính diện tích tứ giác ABCD, biết rằng AB vuông góc với CD, AB=6 cm, BC=15cm, CD=8cm,DA=5cm
Các bạn giải giúp mk nha. Hiện giờ mk đg cần gấp. Có thể xong trước 6h chiều nay đc ko. Mk cảm ơn các bạn trước nhé!!