Giá trị lớn nhất của: \(y=x^3+5x+7\) trên đoạn \([-5:0]\)bằng:
A. 80
B. -143
C. 5
D. 7
Những câu hỏi liên quan
Cho hàm số y=x^3 +5x+7. Giá trị lớn nhất của hàm số trên đoạn [-5;0] bằng bao nhiêu?
A. 5
B. 7
C. 80
D. -143
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y x2 trên đoạn [-3; 0];
b) y x+1x−1�+1�−1 trên đoạn [3; 5].
Đọc tiếp
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y = x2 trên đoạn [-3; 0];
b) y = trên đoạn [3; 5].
Cho hàm số y = x 3 + 5 x + 7 . Giá trị lớn nhất của hàm số trên đoạn - 5 ; 0 bằng bao nhiêu?
A. 5
B. 7
C. 80
D. -143
Giá trị nhỏ nhất của hàm số f(x) = x 3 + 3 x 2 - 9x - 7 trên đoạn [-4;3] bằng:
A. -5 B. 0
C. 7 D. -12
Đáp án: D.
Ta có f(x) = x 3 + 3 x 2 - 9x - 7 ⇒ f'(x) = 3 x 2 + 6x - 9 = 0
⇔ 
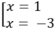
f(-4) = 13, f(-3) = 30, f(1) = -12, f(3) = 20
Vậy min f(x) = -12.
Đúng 0
Bình luận (0)
Giá trị nhỏ nhất của hàm số f(x) = x 3 + 3 x 2 - 9x - 7 trên đoạn [-4;3] bằng:
A. -5 B. 0
C. 7 D. -12
Đáp án: D.
Ta có f(x) = x 3 + 3 x 2 - 9x - 7 ⇒ f'(x) = 3 x 2 + 6x - 9 = 0
⇔ 
f(-4) = 13, f(-3) = 30, f(1) = -12, f(3) = 20
Vậy min f(x) = -12.
Đúng 0
Bình luận (0)
Giá trị lớn nhất của x thỏa mãn phương trình 7 x 2 (x – 7) + 5x( 7 – x) = 0 là
A. x = 5 7
B. x = 7
C. x = 0
D. x = 8
7 x 2 (x – 7) + 5x(7 – x) = 0
ó 7x.x(x – 7) – 5.x(x – 7) = 0
ó (7x.x – 5.x)(x – 7) = 0
ó x(7x – 5)(x – 7) = 0
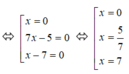
Giá trị lớn nhất của x thỏa mãn đề bài là x = 7.
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
1 . Tìm x biết :
a ] |x - 2,1| = 3/2
b ] (x + 5) . (2x - 3) = 0
2 . Tìm giá trị nhỏ nhất của :
a ] A = 2 . | 2 - 5x | - 4/6
b ] B = | x - 1/2 | + | y - 3/4 | - 1,5
3 . Tìm giá trị lớn nhất của :
a ] P = 7 - 1/2 | 5-x |
b ] Q = - 14 - 2 | x + 3 | -3 | y - 1 |
1,
a,
Ta có:
|x-2,1|=3/2
TH1: x-2,1=3/2
=> x=-3/5
TH2: 2,1-x=3/2
=> x=3/5
b, (x + 5) . (2x - 3) = 0
=> \(\orbr{\begin{cases}x+5=0\\2x-3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-5\\x=\frac{3}{2}\end{cases}}\)
2,
a, A = 2 . | 2 - 5x | - 4/6
b, B = | x - 1/2 | + | y - 3/4 | - 1,5
Giải:
a,
Ta có: \(\left|\text{ 2-5x}\right|\ge0\Rightarrow2.\left|2-5x\right|\ge0\)
\(\Rightarrow2.\left|2-5x\right|-\frac{4}{6}\ge-\frac{4}{6}\)
Dấu '=' xảy ra khi 2.|2-5x|=0
=> \(x=\frac{2}{5}\)
Min A=-4/6 khi và chỉ khi x=2/5
b, B = | x - 1/2 | + | y - 3/4 | - 1,5
Tương tự Min B= -1,5 khi và chỉ khi x=... y=... tự giải
Đúng 0
Bình luận (0)
Câu 3:
a,
Ta có:
\(\frac{1}{2}.\left|5-x\right|\ge0\)
=> \(7-\frac{1}{2}\left|5-x\right|\le7\)
Dấu '=' xảy ra khi
|5-x|=0
=> x=5
câu b tương tự
Đúng 0
Bình luận (0)
Bạn Sáng giải giùm mình bài toán hình mà mình mới ra lun nha
Đúng 0
Bình luận (0)
Giá trị của biểu thức A=x^5 - 5x^4 + 5x^3 - 5x^2 + 5x tại x=4 bằng:
A.3 B.-3 C.4 D.-14
I) THỰC HIỆN PHÉP TÍNH a) 2x(x^2-4y) b)3x^2(x+3y) c) -1/2x^2(x-3) d) (x+6)(2x-7)+x e) (x-5)(2x+3)+x II phân tích đa thức thành nhân tử a) 6x^2+3xy b) 8x^2-10xy c) 3x(x-1)-y(1-x) d) x^2-2xy+y^2-64 e) 2x^2+3x-5 f) 16x-5x^2-3 g) x^2-5x-6 IIITÌM X BIẾT a)2x+10 b) -3x-50 c) -6x+70 d)(x+6)(2x+1)0 e)2x^2+7x+30 f) (2x-3)(2x+1)0 g) 2x(x-5)-x(3+2x)26 h) 5x(x-1)x-1 IV TÌM GTNN,GTLN. a) tìm giá trị nhỏ nhất x^2-6x+10 2x^2-6x b) tìm giá trị lớn nhất 4x-x^2-5 4x-x^2+3
Đọc tiếp
I) THỰC HIỆN PHÉP TÍNH a) 2x(x^2-4y) b)3x^2(x+3y) c) -1/2x^2(x-3) d) (x+6)(2x-7)+x e) (x-5)(2x+3)+x II phân tích đa thức thành nhân tử a) 6x^2+3xy b) 8x^2-10xy c) 3x(x-1)-y(1-x) d) x^2-2xy+y^2-64 e) 2x^2+3x-5 f) 16x-5x^2-3 g) x^2-5x-6 IIITÌM X BIẾT a)2x+1=0 b) -3x-5=0 c) -6x+7=0 d)(x+6)(2x+1)=0 e)2x^2+7x+3=0 f) (2x-3)(2x+1)=0 g) 2x(x-5)-x(3+2x)=26 h) 5x(x-1)=x-1 IV TÌM GTNN,GTLN. a) tìm giá trị nhỏ nhất x^2-6x+10 2x^2-6x b) tìm giá trị lớn nhất 4x-x^2-5 4x-x^2+3
Giải như sau.
(1)+(2)⇔x2−2x+1+√x2−2x+5=y2+√y2+4⇔(x2−2x+5)+√x2−2x+5=y2+4+√y2+4⇔√y2+4=√x2−2x+5⇒x=3y(1)+(2)⇔x2−2x+1+x2−2x+5=y2+y2+4⇔(x2−2x+5)+x2−2x+5=y2+4+y2+4⇔y2+4=x2−2x+5⇒x=3y
⇔√y2+4=√x2−2x+5⇔y2+4=x2−2x+5, chỗ này do hàm số f(x)=t2+tf(x)=t2+t đồng biến ∀t≥0∀t≥0
Công việc còn lại là của bạn !
Đúng 1
Bình luận (0)
\(\left(x+6\right)\left(2x+1\right)=0\)
<=> \(\orbr{\begin{cases}x+6=0\\2x+1=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=-6\\x=-\frac{1}{2}\end{cases}}\)
Vậy....
hk tốt
^^
Đúng 1
Bình luận (0)