Đáp án: D.
Ta có f(x) = x 3 + 3 x 2 - 9x - 7 ⇒ f'(x) = 3 x 2 + 6x - 9 = 0
⇔ 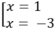
f(-4) = 13, f(-3) = 30, f(1) = -12, f(3) = 20
Vậy min f(x) = -12.
Đáp án: D.
Ta có f(x) = x 3 + 3 x 2 - 9x - 7 ⇒ f'(x) = 3 x 2 + 6x - 9 = 0
⇔ 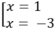
f(-4) = 13, f(-3) = 30, f(1) = -12, f(3) = 20
Vậy min f(x) = -12.
Giá trị nhỏ nhất của hàm số f(x) = x 3 + 3 x 2 - 9x - 7 trên đoạn [-4;3] bằng:
A. -5 B. 0
C. 7 D. -12
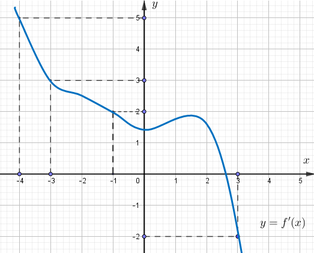
Cho hàm số f(x). Biết hàm số y=f '(x) có đồ thị như hình bên. Trên đoạn [-4;3], hàm số g ( x ) = 2 f ( x ) + ( 1 - x ) 2 đạt giá trị nhỏ nhất tại điểm
A.![]() .
.
B.![]() .
.
C.![]() .
.
D.![]() .
.
Cho hàm số f(x). Biết hàm số y = f'(x) có đồ thị như hình bên.
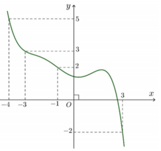
Trên đoạn [-4;3] hàm số g ( x ) = 2 f ( x ) + 1 - x 2 đạt giá trị nhỏ nhất tại điểm
![]()
![]()
![]()
![]()
Giá trị nhỏ nhất của hàm số f(x) = x +1/x trên nửa khoảng [2;+••] A:2 B:5/2 C:0 D:7/2
Cho hàm số f(x). Biết hàm số y = f'(x) có đồ thị như hình bên. Trên đoạn [-4;3], hàm số g(x) = 2f(x) + 1 - x 2 đạt giá trị nhỏ nhất tại điểm
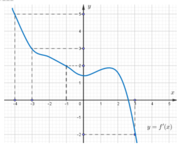
A. x 0 = -4
B. x 0 = -1
C. x 0 = 3
D. x 0 = -3
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x)= x^3-3x^2+2 trên đoạn [-1,2] . Tính giá trị biểu thức P= M-2m A. 3√2-3 B. 2√2-5 C. 3√3-5 D. 3√3-3
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau trên đoạn [2;4]
f ( x ) = x + 9 x
(Đề thi tốt nghiệp THPT năm 2008)
Cho hàm số f(x) có đồ thị của hàm số f'(x) như hình vẽ. Biết f(0) + f(1) - 2f(2) = f(4) - f(3). Giá trị nhỏ nhất m, giá trị lớn nhất M của hàm số f(x) trên đoạn [0;4] là
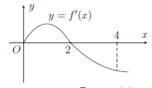
A. m = f(4), M = f(1)
B. m = f(4), M = f(2)
C. m = f(1), M = f(2)
D. m = f(0), M = f(2)