tìm m để hàm số sau đồng biến trên
A,y=1/3x3-x2+m2x-m3+1
Tìm các giá trị của m để hàm số y = x - m 2 x - 3 m + 2 đồng biến trên khoảng - ∞ ; 1 .
A. m ∈ - ∞ ; 1 ∪ 2 ; + ∞
B. m ∈ - ∞ ; 1
C. m ∈ 1 ; 2
D. m ∈ 2 ; + ∞
Tìm tất cả các giá trị nguyên của tham số m để hàm số y = m 2 x − 4 x − 1 đồng biến trên từng khoảng xác định:
A. m = 1 ; m = 2 ; m = 3
B. m = 0 ; m = − 1 ; m = − 2
C. m = − 1 ; m = 0 ; m = 1
D. m = 0 ; m = 1 ; m = 2
Đáp án C
Ta có y ' = 4 − m 2 x − 1 2 hàm số đồng biến trên tập xác định của nó
⇔ 4 − m 2 > 0 ⇔ − 2 < m < 2 do m nguyên ⇒ m = 0, m = ± 1
Bài 2. Tìm m để mỗi hàm số sau đây đồng biến hoặc nghịch biến
a) y=(m-1)x+2
b) y= -m2x+1
c) y=(1-3m)x+2m
a) Để hàm đồng biến <=> a>0 <=> m-1>0 <=> m>1
Để hàm nghịch biến <=> a<0 <=> m<1
b)Có phải đề như này: \(y=-m^2x+1\)
Nhận xét: \(-m^2\le0\forall m\)
=> Hàm luôn nghịch biến với mọi \(m\ne0\)
c)Để hàm nghịch biến <=> a<0 <=> 1-3m<0\(\Leftrightarrow m>\dfrac{1}{3}\)
Để hàm đồng biền <=> a>0 \(\Leftrightarrow m< \dfrac{1}{3}\)
a/ Hàm số y=(m-1)x+2 đồng biến khi và chỉ khi m-1>0
⇔m>1
nghịch biến khi và chỉ khi m-1<0
⇔m<1
b/Hàm số y=-2mx+1 đồng biến khi và chỉ khi -2m>0
⇔m<0
nghịch biến khi và chỉ khi -2m<0
⇔m>0
c/Hàm số y=(1-3m)x+2m đồng biến khi và chỉ khi 1-3m>0
⇔-3m>-1
⇔m<\(\dfrac{1}{3}\)
nghịch biến khi và chỉ khi 1-3m<0
⇔-3m<-1
⇔m>\(\dfrac{1}{3}\)
Tìm m để hàm số y = x 2 − 4 2 x + m đồng biến trên đồng biến trên 1 ; + ∞ .
A. m ∈ − 4 ; 1 2 \ 0
B. m ∈ − 4 ; 1 2
C. m ∈ 0 ; 1 2
D. m ∈ − 1 2 ; 1 2
Tìm các giá trị của tham số m để hàm số y = x 3 3 - 3 x 2 + m 2 x + 2 m - 3 đồng biến trên R
A. m < -3 hoặc m > 3
B. - 3 ≤ m ≤ 3
C. -3 < m < 3
D. m ≤ - 3 h o ặ c m ≥ 3
Cho hàm số y = x 2 + 2 x x − m . Tìm m để hàm số đồng biến trên − 1 ; + ∞
A. m ∈ − ∞ ; − 1
B. m ≤ 0
C. m ≥ − 1
D. m > − 1
định m để hàm số y=1/3x3 -2x2+mx-2 đồng biến trên tập xác định
Tìm m để hàm số y = x 2 − 4 2 x + m đồng biến trên 1 ; + ∞ .
A. m ∈ − 4 ; 1 2 \ 0
B. m ∈ − 4 ; 1 2
C. m ∈ 0 ; 1 2
D. m ∈ − 1 2 ; 1 2
Đáp án D
Tập xác định
D = − ∞ ; − m ∪ − m ; + ∞ , y ' = x 2 + 2 m x − 4 m 2 x + m 2
TH1:
1 ; + ∞ ⊂ − m ; + ∞ ⇔ Δ ' = m 2 + 4 m < 0 − m < 1 ⇔ − 1 < m < 0
TH2: y'=0 có 2 nghiệm x 1 , x 2 thỏa mãn x 1 ≤ x 2 ≤ 1 và 1 ; + ∞ ⊂ − m ; + ∞
− 2 m 2 ≤ 1 − m < 1 1 − x 1 1 − x 2 ≥ 0 ⇔ 0 ≤ m ≤ 1 2
Kết hợp 2 trường hợp ta được − 1 ≤ m ≤ 1 2
Tìm m để hàm số y = 2 x 4 - ( 3 - m ) x 2 + 1 đồng biến trên - ∞ ; + ∞
![]()
![]()
![]()
![]()
Tìm a ∈ (0; 2 π ) để hàm số sau đồng biến trên khoảng (1; + ∞ ).
y = 1 3 x 3 - 1 2 (1 + cosa) x 2 + 2x cosa + 1
Tập xác định: D = R; y′ = x 2 − (1 + 2cosa)x + 2cosa
y′= 0 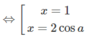
Vì y’ < 0 ở ngoài khoảng nghiệm nên để hàm số đồng biến với mọi x > 1 thì 2cosa ≤ 1
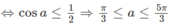
(vì a ∈ (0; 2 π ).