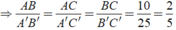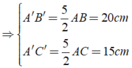Cho tam giác ABC, có AB= 6cm, AC=8cm. Độ dài cạnh BC là:

Những câu hỏi liên quan
Cho tam giác ABC có độ dài các cạnh A B = 8 c m , A C = 8 c m , B C = 6 c m . Tìm góc nhỏ nhất của tam giác?
A. Góc A
B. Góc B
C. Góc C
D. Góc C và B
Do BC là cạnh nhỏ nhất nên góc C là góc nhỏ nhất. Chọn C
Đúng 0
Bình luận (0)
Cho Δ ABC có AB = 8cm, AC = 6cm, BC = 10cm. Tam giác A'B'C' đồng dạng với tam giác ABC có độ dài cạnh lớn nhất là 25 cm. Tính độ dài các cạnh còn lại của Δ A'B'C' ?
A. 4cm; 3cm
B. 7,5cm; 10cm
C. 4,5cm; 6cm
D. 15cm; 20cm
Cho Δ ABC có AB = 8cm,AC = 6cm,BC = 10cm. Tam giác A'B'C' đồng dạng với tam giác ABC có độ dài cạnh lớn nhất là 25 cm. Tính độ dài các cạnh còn lại của Δ A'B'C' ?
A. 4cm; 3cm
B. 7,5cm; 10cm
C. 4,5cm; 6cm
D. 15cm; 20cm
Ta có: Δ ABC đồng dạng Δ A'B'C'
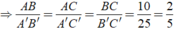
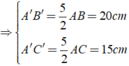
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho tam giác vuông ABC vuông góc tại A. Có cạnh AB dài 6cm, cạnh AC dài 8cm. Tính độ dài cạnh BC.
Cho tam giác ABC vuông tại A có AB < AC ; BI là tia phân giác của góc B ( I∈ AC), vẽ IE BC tại E.
a) Cho biết AB = 6cm; AC = 8cm. Tinh độ dài cạnh BC.
b) Chứng minh tam giác IAE cân.
a) Vì ΔABC là tam giác vuông nên
=> Theo định lý Pytago : Ta có AC2 +AB2 = CB2
Hay 82 + 62 = BC2
BC 2 = 1002
=> BC = 100 cm
b) (đang nghĩ)
Đúng 1
Bình luận (4)
ủa cm IAE cân đc mak anh lại điêu r nek , dễ mak
Đúng 1
Bình luận (3)
Cho tam giác ABC. Lấy D, E trên các cạnh AB, AC sao cho DE // BC và A D = 8 c m , D B = 6 c m , A E = 10 c m . Độ dài cạnh AC là:
A. 8cm
B. 10cm
C. 15cm
D. 17,5cm
Câu 8: Cho tam giác ABC vuông tại A , có AB = 6cm , AC = 8cm, AM là
đường trung tuyến ứng với cạnh BC . Độ dài của cạnh AM là :
A. 10cm
B. 9cm
C. 5cm
D. 8cm
Xét \(\Delta ABC\) vuông tại \(A\) có:
\(BC^2=AB^2+AC^2\) (định lí pitago)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét \(\Delta ABC\) vuông tại \(A\) có:
\(AM\) là đường trung tuyến ứng với cạnh huyền \(BC\) (định lí đường trung tuyến ứng với cạnh huyền trong tam giác vuông)
\(\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{1}{2}.10=5\left(cm\right)\)
\(\Rightarrow\) Chọn đáp án \(C\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
B. Phần tự luận (7 điểm)
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm.
a. Tính độ dài cạnh BC
a. Áp dụng định lí Pytago trong tam giác ABC ta có:
BC2 = AB2 + AC2 = 62 + 82 = 100 ⇒ BC = 10cm
Đúng 0
Bình luận (0)
Cho tam giác vuông ABC vuông tại A. Biết độ dài ba cạnh là: AB=6cm, AC=8cm và BC=10cm. Tính chiều cao tương ứng với cạnh đáy BC
Gọi AH là cc tương ứng với BC
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\)
Đúng 0
Bình luận (0)