mấy bn giúp mik vs
2/Cho hình vẽ sau. Chứng minh rằng: A1+ACM=B1+BMC
Cho hình vẽ sau. Chứng minh A1 + ACM = B1 + BMC
Mình bổ sung thêm là a vuông góc với c nha
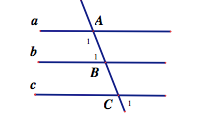
Cho hình vẽ. Biết A1 + B1 = 180độ , B1 = C1. Chứng minh rằng A//B//C ?
\(\hat{A}_1+\hat{B}_1=180^o\Rightarrow a\text{ // }b\left(tcp\right)\)
\(\hat{B}_1=\hat{C}_1\Rightarrow b\text{ // }c\left(đv\right)\)
\(\Rightarrow a\text{ // }b\text{ // }c\left(đpcm\right)\)
Cho hình vẽ bên biết : A2 + A3 + B1 = 240 độ và A1 = 120 độ
a, Chứng minh rằng a || b
b, Chứng minh rằng a vuông góc b
Cho hình vẽ, biết a1 - a2 = b1 - b2. Chứng minh rằng a//b
Cho 5 số nguyên a1,a2,a3,a4,a5 . Gọi b1,b2,b3,b4,b5 là hoán vị của 5 đã số đã cho . Chứng minh rằng tích (a1 - b1 ).(a2 -b2).(a3 - b3).(a4 - a4).(a5 - b5) chia hết cho 2
Các bạn giúp mik thì mik cảm ơn rất nhìu <3
Cho A1=B1 Chứng minh a)A1=B3, A4=B2 b)A2=B2, A3=B3, A4=B4 c)A2+B1=180°,A4+B3=180°
giúp mik vs
a, \(\widehat{B}_1=\widehat{B_3}\) đối đỉnh
\(\widehat{A}_1=\widehat{B}_1\) theo bài đầu
Do đó \(\widehat{A_1}=\widehat{B_3}\)
Mặt khác,ta có \(\widehat{A_1}+\widehat{A_4}=180^0\) hai góc kề bù
=> \(\widehat{A_4}=180^0-\widehat{A_1}\) \((1)\)
Và \(\widehat{B_2}+\widehat{B_3}=180^0\) hai góc kề bù
=> \(\widehat{B_2}=180^0-\widehat{B_3}\) \((2)\)
\(\widehat{A_1}=\widehat{B_3}\) \((3)\)
Từ 1,2,3 ta có : \(\widehat{A_4}=\widehat{B_2}\)
b, \(\widehat{A_2}=\widehat{A_4}\) đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) theo câu a
Do đó : \(\widehat{A_2}=\widehat{B_2};\widehat{A_1}=\widehat{A_3}\) đối đỉnh
\(\widehat{A_1}=\widehat{B_3}\) câu a
Do đó \(\widehat{A_3}=\widehat{B_3}\). Mặt khác \(\widehat{B_2}=\widehat{B_4}\) hai góc đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) câu a . Do đó \(\widehat{A_4}=\widehat{B_4}\)
c, \(\widehat{B_1}+\widehat{B_2}=180^0\) hai góc kề bù
\(\widehat{A_1}=\widehat{B_1}\) theo đầu bài
Do đó \(\widehat{A_1}+\widehat{B_2}=180^0\)
Mặt khác \(\widehat{B_2}+\widehat{B_3}=180^0\) kề bù
\(\widehat{A_4}=\widehat{B_2}\) theo câu a . Do đó \(\widehat{A_4}+\widehat{B_3}=180^0\)
Cho hình 3, biết: A 1 ^ = B 1 ^ và C 1 ^ = C 2 ^ . Chứng minh rằng m ⊥ b
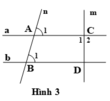
Ta có: A 1 ^ = B 1 ^ (gt).
Þ a / / b (vì có cặp góc đồng vị bằng nhau).
Mặt khác, C 1 ^ + C 2 ^ = 180 o (kề bù)
mà C 1 ^ = C 2 ^ (gt) nên C 1 ^ = 180 o : 2 = 90 o .
Vậy m ⊥ a .
Cho hình vẽ bên biết B1=75 độ
a)chứng minh m//n
b)Tính A1 và A2
a: m vuông góc c
n vuông góc c
=>m//n
b: góc A1=180-75=105 độ
góc A2=180-105=75 độ
Cho hình vẽ biết góc A1 =góc B1 =70°.Chứng minh a//b
Các bạn giải hộ mình với ạ mình đang cần gấp.
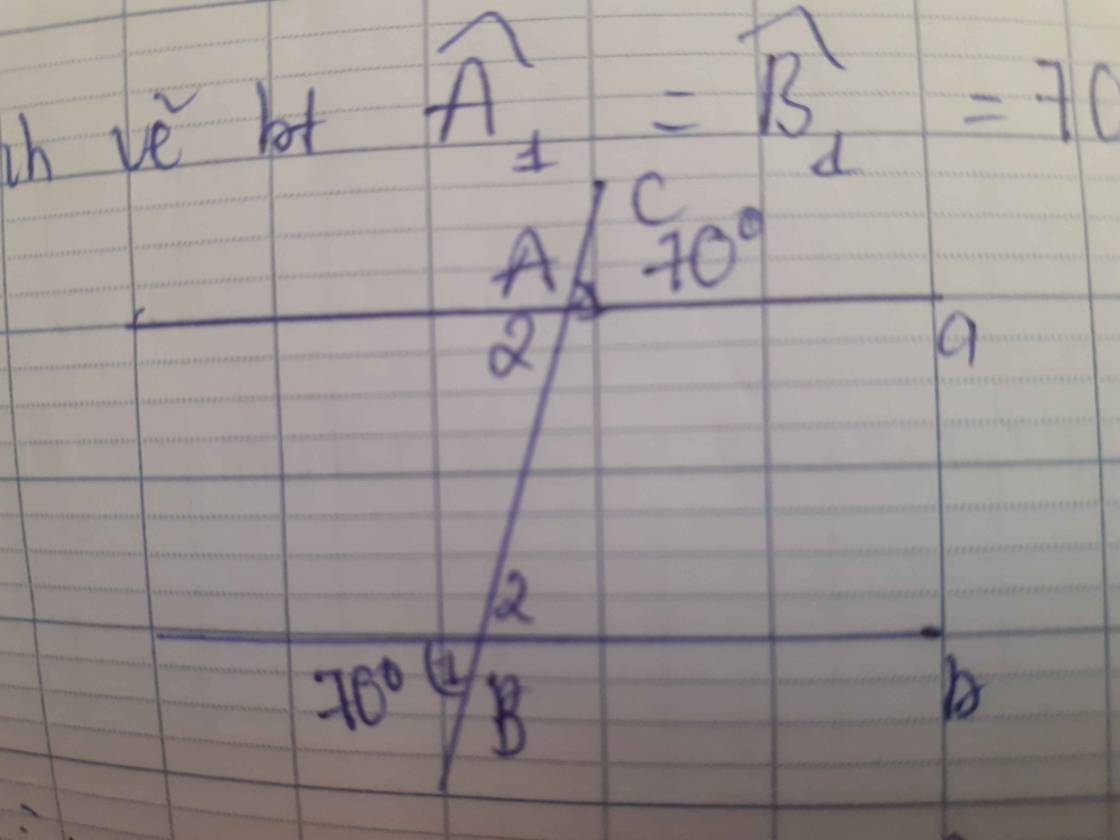
Ta có:
∠B₂ = ∠B₁ = 70⁰ (đối đỉnh)
⇒ ∠B₂ = ∠A₁ = 70⁰
Mà ∠B₂ và ∠A₁ là hai góc đồng vị
⇒ a // b