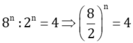tìm n biết: 10-8n/2n+3

Những câu hỏi liên quan
Tìm n∈Z biết
a) 2n+1⋮3-n
b)8n+1⋮2-n
c)3n+4⋮2-n
d)2n+1⋮2n+2
e)3-4n⋮2n+1
e: \(\Leftrightarrow2n+1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{0;-1;2;-3\right\}\)
Đúng 0
Bình luận (0)
Tìm n nguyên biết:8n+3 chia hết cho 2n-1
tìm tập hợp số tự nhiên n biết 8n+27/2n+3 là số tự nhiên S
8n+27 = 8n+12 +15 =4(2n+3)+15 chia hết chó 2n+3
=> 15 chia hết cho 2n+3
2n+3 thuộc ước của 15; U(15) ={1;3;5;15}
+2n+3 = 1 loại
+2n+3 =3 => n =0
+2n+3 =5 => n=1
+2n+3 =15=> n =6
Vậy n thuộc {0;1;6}
Đúng 0
Bình luận (0)
8n+27 = 8n+12 +15 =4(2n+3)+15 chia hết cho 2n+3
=> 15 chia hết cho 2n+3
2n+3 thuộc ước của 15; U(15) ={1;3;5;15}
+2n+3 = 1 loại
+2n+3 =3 => n =0
+2n+3 =5 => n=1
+2n+3 =15=> n =6
Vậy n thuộc {0;1;6}
Đúng 0
Bình luận (0)
Tìm số tự nhiên n, biết : 8 n : 2 n = 4
Tìm các giới hạn sau:
\(a,lim\dfrac{\sqrt[3]{8n^3+2n}}{-n+3}\)
\(b,lim\dfrac{\left(2n\sqrt{n}+1\right)\left(\sqrt{n}+3\right)}{\left(n-1\right)\left(3-2n\right)}\)
\(a,lim\dfrac{^3\sqrt{8n^3+2n}}{-n+3}\)
\(=lim\dfrac{^3\sqrt{8+\dfrac{2}{n^2}}}{-1+\dfrac{3}{n}}=\dfrac{^3\sqrt{8}}{-1}=\dfrac{2}{-1}=-2\)
Đúng 1
Bình luận (0)
\(\lim\dfrac{\left(2n\sqrt{n}+1\right)\left(\sqrt{n}+3\right)}{\left(n-1\right)\left(3-2n\right)}=\lim\dfrac{\left(2+\dfrac{1}{n\sqrt{n}}\right)\left(1+\dfrac{3}{\sqrt{n}}\right)}{\left(1-\dfrac{1}{n}\right)\left(\dfrac{3}{n}-2\right)}=\dfrac{2.1}{1.\left(-2\right)}=-1\)
Đúng 1
Bình luận (0)
tìm số nguyên n,biết
8n-9 là bội của 2n+5
tìm n để n+3 =2n+6/6=8n+3/2 đều là số nguyên
ta có: \(n+3=\frac{2n+6}{6}=\frac{8n+3}{2}=\frac{6n+18}{6}=\frac{2n+6}{6}=\frac{24n+9}{6}\)
\(\Rightarrow6n+18=2n+6=24n+9\)
\(\Rightarrow6n+18-2n-6-24n-9=0\)
6n -2n-24n + 18-6-9 = 0
n. ( 6-2-24) + ( 18-6-9) = 0
n.( -20) + 3 = 0
n . (-20) = -3
n = -3/ -20
n= 3/20
p/s nha!
Đúng 0
Bình luận (0)
B1
a) Tìm ước chung của n+1; 3n+2(n thuộc N)
b) Tìm ước chung của 2n+3 và 3n+4 (n thuộc N)
B2 Biết rằng 2 số 5n+6 và 8n+7 không phải là 2 số nguyên tố cùng nhau. tìm ước chung lớn nhất ( 5n+6; 8n+7) n thuộc N
Tìm x thuộc N để (8n+21) chia hết cho (2n+3)