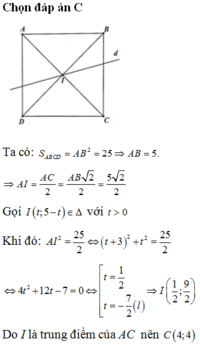Trong mặt phẳng Oxy, cho hình vuông ABCD có tâm I. Biết E(2;3), F(-2;1) lần luợt là trung điểm của BC, ID và điểm A có tung độ dương. Tìm toạ độ trọng tâm G của tam giác ABC
Những câu hỏi liên quan
Trong mặt phẳng Oxy, cho hình vuông ABCD có đình M(-–-3;5), tâm I thuộc đường thẳng d : y =−x+5 và diện tích của hình vuông ABCD bằng 25 . Tim tọa độ các đỉnh của hình vuông ABCD, biết rằng tâm I có hoành độ dương
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có đỉnh A(-3;5), tâm I thuộc đường thẳng
∆
:
x
+
y
-
5
0
và diện tích hình vuông bằng 25. Tìm tọa độ đỉnh C, biết rằng tâm I có hoành độ dương.
Đọc tiếp
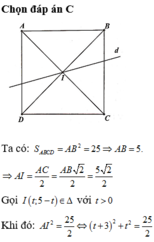
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có đỉnh A(-3;5), tâm I thuộc đường thẳng ∆ : x + y - 5 = 0 và diện tích hình vuông bằng 25. Tìm tọa độ đỉnh C, biết rằng tâm I có hoành độ dương.
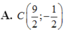
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có đỉnh A(-3;5), tâm I thuộc đường thẳng
∆
:
x
+
y
-
5
0
và diện tích hình vuông bằng 25. Tìm tọa độ đỉnh C, biết rằng tâm I có hoành độ dương A.
C
9
2
;
-
1
2
B. C(1;8) C. C(4;4)...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có đỉnh A(-3;5), tâm I thuộc đường thẳng ∆ : x + y - 5 = 0 và diện tích hình vuông bằng 25. Tìm tọa độ đỉnh C, biết rằng tâm I có hoành độ dương
A. C 9 2 ; - 1 2
B. C(1;8)
C. C(4;4)
D. C(2;2)
trong mặt phẳng oxy cho hình vuông ABCD có tâm I(2:2) là giao điểm hai đường chéo. Lấy M thuộc DC sao cho DC=4DM , biết đường thẳng AM có phương trình :7x + 6y -11= 0. Viết phương trình đường tròn (C) ngoại tiếp hình vuông ABCD
Trong mặt phẳng với hệ tọa độ vuông góc Oxy cho ba điểm I(1;1) J(-2;2) K(2;-2).Tìm tọa độ các đỉnh của hình vuông ABCD sao cho I là tâm hình vuông, J thuộc cạnh AB và K thuộc cạnh CD.
Trong mặt phẳng Oxy, cho bốn điểm \(A(2;1),B(1;4),C(4;5),D(5;2)\)
a) Chứng minh ABCD là một hình vuông
b) Tìm tọa độ tâm I của hình vuông ABCD
a) Ta có: \(\overrightarrow {AB} = ( - 1;3),\overrightarrow {BC} = (3;1),\overrightarrow {CD} = (1; - 3),\overrightarrow {DA} = ( - 3; - 1)\)
Suy ra \(AB = BC = CD = DA = \sqrt {10} \)
Mặt khác \(\overrightarrow {AB} .\overrightarrow {BC} = ( - 1).3 + 3.1 = 0 \Rightarrow AB \bot BC\)
Vậy ABCD là hình vuông
b) Ta có ABCD là hình vuông, nên tâm I là trung điểm của đoạn thẳng AC
Vậy tọa độ điểm I là \(I(3;3)\)
Đúng 0
Bình luận (0)
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB 2AM, phương trình đường phân giác trong AD : x-y 0, phương trìn đường cao CH: 2x+y+3 0. Tìm tọa độ các đỉnh A,B,C.2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC 2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y0,điểm A có hoành độ dương
Đọc tiếp
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB =2AM, phương trình đường phân giác trong AD : x-y =0, phương trìn đường cao CH: 2x+y+3 =0. Tìm tọa độ các đỉnh A,B,C.
2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC =2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y=0,điểm A có hoành độ dương
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD A. B. C. D.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD
A. 
B. 
C. 
D. 
trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có đỉnh A(-1,2) và tâm I(1/2:0) xác định tọa độ các đỉnh còn lại của hình chữ nhật ABCD, biết đường thẳng BC đi qua điểm m(4;-3)
I là trung điểm AC \(\Rightarrow C\left(2;-2\right)\)
\(\Rightarrow\overrightarrow{CM}=\left(2;-1\right)\Rightarrow\) đường thẳng BC có dạng:
\(1\left(x-2\right)+2\left(y+2\right)=0\Leftrightarrow x+2y+2=0\)
Đường thẳng AB qua A và vuông góc BC nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow2x-y+4=0\)
B là giao điểm AB và BC nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}x+2y+2=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(...\right)\)
I là trung điểm BD \(\Rightarrow\left\{{}\begin{matrix}x_D=2x_I-x_B=...\\y_D=2y_I-y_B=...\end{matrix}\right.\)
Đúng 0
Bình luận (0)