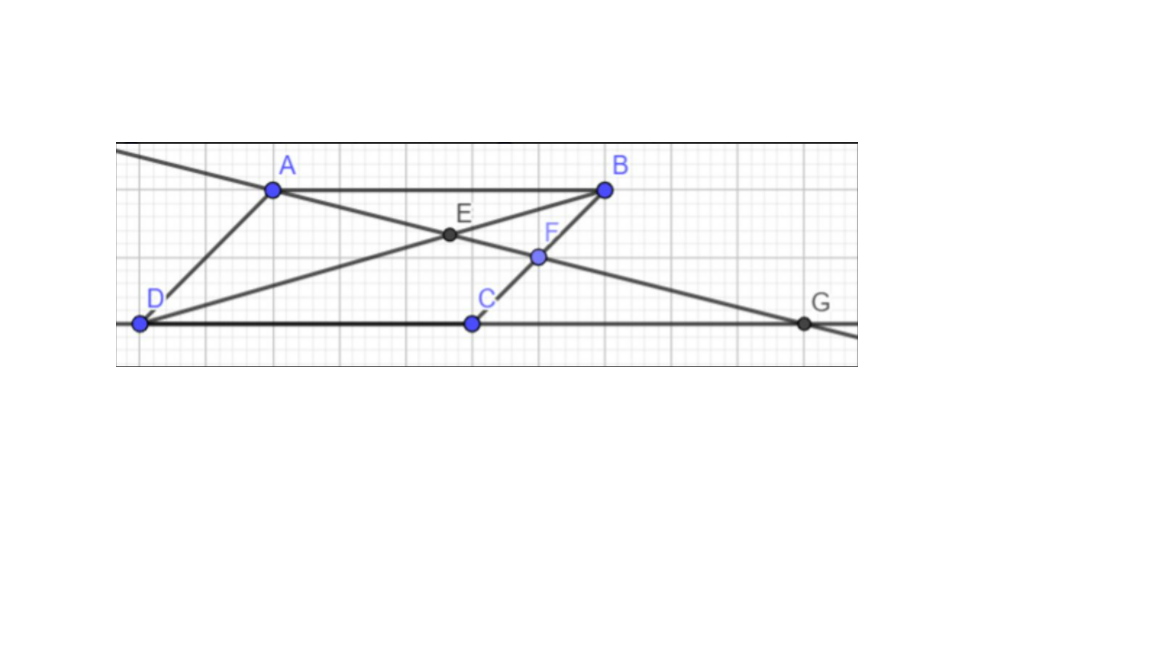
Cho hình bình hành ABCD. Qua điểm A ta kẻ một đường thẳng bất kì cắt đoạn thẳng BD, BC, CD lần lượt tại E, F, G. CMR
a.△DEA đồng dạng vs △ BFE
b.AB. AG=AF. DG
c, AE2 =AF. EG
d, tích BF.DG không đổi
e. Cho AB=10cm,AD=9cm, DG=6cm. Tính độ dài đoạn thẳng BF và chứng minh 9S△BEA= 25S△DEG
Giải giúp mk câu e