x= 1/2 x=2 x=3/2

\(4x^3-16x^2+19x-6=0\)

\(\Leftrightarrow4x^3-8x^2-8x^2+16x+3x-6=0\)

\(\Leftrightarrow\left(x-2\right)\left(4x^2-8x+3\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(2x-3\right)\left(2x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{3}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\)

a) \(4x^2+16x+3=0\)

\(\Delta'=84-12=72\Rightarrow\sqrt[]{\Delta'}=6\sqrt[]{2}\)

Phương trình có 2 nghiệm

\(\left[{}\begin{matrix}x=\dfrac{-8+6\sqrt[]{2}}{4}\\x=\dfrac{-8-6\sqrt[]{2}}{4}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-2\left(4-3\sqrt[]{2}\right)}{4}\\x=\dfrac{-2\left(4+3\sqrt[]{2}\right)}{4}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-\left(4-3\sqrt[]{2}\right)}{2}\\x=\dfrac{-\left(4+3\sqrt[]{2}\right)}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3\sqrt[]{2}-4}{2}\\x=\dfrac{-3\sqrt[]{2}-4}{2}\end{matrix}\right.\)

b) \(7x^2+16x+2=1+3x^2\)

\(4x^2+16x+1=0\)

\(\Delta'=84-4=80\Rightarrow\sqrt[]{\Delta'}=4\sqrt[]{5}\)

Phương trình có 2 nghiệm

\(\left[{}\begin{matrix}x=\dfrac{-8+4\sqrt[]{5}}{4}\\x=\dfrac{-8-4\sqrt[]{5}}{4}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-4\left(2-\sqrt[]{5}\right)}{4}\\x=\dfrac{-4\left(2+\sqrt[]{5}\right)}{4}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\left(2-\sqrt[]{5}\right)\\x=-\left(2+\sqrt[]{5}\right)\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-2+\sqrt[]{5}\\x=-2-\sqrt[]{5}\end{matrix}\right.\)

c) \(4x^2+20x+4=0\)

\(\Leftrightarrow4\left(x^2+5x+1\right)=0\)

\(\Leftrightarrow x^2+5x+1=0\)

\(\Delta=25-4=21\Rightarrow\sqrt[]{\Delta}=\sqrt[]{21}\)

Phương trình có 2 nghiệm

\(\left[{}\begin{matrix}x=\dfrac{-5+\sqrt[]{21}}{2}\\x=\dfrac{-5-\sqrt[]{21}}{2}\end{matrix}\right.\)

Tích mình đi rồi mình nói thề bạn

e: ta có: \(4x^2+4x-6=2\)

\(\Leftrightarrow4x^2+4x-8=0\)

\(\Leftrightarrow\left(x+2\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)

f: Ta có: \(2x^2+7x+3=0\)

\(\Leftrightarrow\left(x+3\right)\left(2x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-\dfrac{1}{2}\end{matrix}\right.\)

Rảnh rỗi thật sự .-.

a) x^4 - 2x^2 + 1 = 0 

=> ( x^2 - 1 )^2 = 0 

=> x^2 - 1 = 0 

=> x^2 = 1 

=> x = 1 hoặc x = -1 

a) x⁴-2x²+1=0

(thang Tran giải rồi nhé)

b) x⁴-2x²-8=0

<=> x^4 - 2x^2 +1 -9 =0 

<=>  (x^2 -1)^2 -9 =0

\(\Leftrightarrow\orbr{\begin{cases}x^2-1=-3\\x^2-1=3\end{cases}\Leftrightarrow\orbr{\begin{cases}x^2=-2\left(VN\right)\\x=+_-\sqrt{2}\end{cases}}}\)

Vậy x=+- căn 2

c) x⁴-4x²-60=0

\(\Leftrightarrow x^4-4x^2+4-64=0\)

\(\Leftrightarrow\left(x^2-2\right)-64=0\)

\(\Leftrightarrow\left(x^2+62\right)\left(x^2-66\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x^2+62=0\\x^2-66=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x^2=-62\left(VN\right)\\x^2=+_-\sqrt{66}\end{cases}}}\)

Vậy x=+- căn 66

d) x⁶-16x²+64=0

a) √16x = 8 (điều kiện: x ≥ 0)

⇔ 16x = 82 ⇔ 16x = 64 ⇔ x = 4

(Hoặc: √16x = 8 ⇔ √16.√x = 8

⇔ 4√x = 8 ⇔ √x = 2 ⇔ x = 4)

b) điều kiện: x ≥ 0

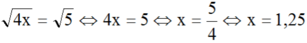
c) điều kiện: x - 1 ≥ 0 ⇔ x ≥ 1 (*)

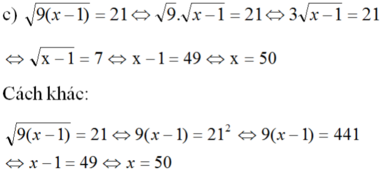
x = 50 thỏa mãn điều kiện (*) nên x = 50 là nghiệm của phương trình.

d) Vì (1 - x)2 ≥ 0 ∀x nên phương trình xác định với mọi giá trị của x.

- Khi 1 – x ≥ 0 ⇔ x ≤ 1

Ta có: 2|1 – x| = 6 ⇔ 2(1 – x) = 6 ⇔ 2(1 – x) = 6

⇔ –2x = 4 ⇔ x = –2 (nhận)

- Khi 1 – x < 0 ⇔ x > 1

Ta có: 2|1 – x| = 6 ⇔ 2[– (1 – x)] = 6

⇔ x – 1 = 3 ⇔ x = 4 (nhận)

Vậy phương trình có hai nghiệm: x = - 2; x = 4

\(a.\left(x^3-16x\right)=0\)

\(\Leftrightarrow x\left(x^2-16\right)=0\)

\(\Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\)

\(\Leftrightarrow\hept{\begin{cases}x=0\\x-4=0\\x+4=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\x=4\\x=-4\end{cases}}}\)

Uầy lười lm waa

. Hãy nhiệt tình lên :>> Chúng ta là công dân cùng một nước,phải giúp đỡ nhau a~~~

a) \(x^3-16x=0\)

 ⇔\(x\left(x^2-16\right)=0\)

 ⇒\(x=0\) hoặc \(x^2-16=0\)

\(TH_1:x=0\)

\(TH_2:x^2-16=0\) ⇔ \(x^2=16\) ⇔ \(x=\pm4\)

             Vậy \(x\in\left\{0;\pm4\right\}\)

b) \(\left(2x+1\right)^2-\left(x-1\right)^2=0\)

⇒ \(2x+1=x-1\)

⇒ \(2x+2=x\)

⇒ \(2\left(x+1\right)=x\) ⇒ x = -2 

        Vậy x = -2

           Bài làm :

\(a\text{)}3x^2+4x=0\Leftrightarrow x\left(3x+4\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\3x+4=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=-\frac{4}{3}\end{cases}}\)

\(b\text{)}25x^2-0,64=0\Leftrightarrow\left(5x-0,8\right)\left(5x+0,8\right)=0\Leftrightarrow\orbr{\begin{cases}5x-0,8=0\\5x+0,8=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0,16\\-0,16\end{cases}}\)

\(c\text{)}x^4-16x^2=0\Leftrightarrow\left(x^2-4x\right)\left(x^2+4x\right)=0\Leftrightarrow\orbr{\begin{cases}x^2-4x=0\\x^2+4x=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x\left(x-4\right)=0\\x\left(x+4\right)=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm4\end{cases}}\)

\(d\text{)}x^2+x=6\Leftrightarrow x^2+x-6=0\Leftrightarrow\left(x^2-2x\right)+\left(3x-6\right)=0\Leftrightarrow x\left(x-2\right)+3\left(x-2\right)=0\Leftrightarrow\left(x+3\right)\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x+3=0\\x-2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-3\\x=2\end{cases}}\)

Bài làm :

\(a)3x^2+4x=0\)

\(\Rightarrow x\left(3x+4\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x=0\\3x+4=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=\frac{-4}{3}\end{cases}}\)

Vậy x = 0 hoặc \(x=\frac{-4}{3}\) .

\(b)25x^2-0,64=0\)

\(\Rightarrow\left(5x\right)^2=\frac{16}{25}\)

\(\Rightarrow\left(5x\right)^2=\left(\frac{4}{5}\right)^2\)

\(\Rightarrow\orbr{\begin{cases}5x=\frac{4}{5}\\5x=\frac{-4}{5}\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{4}{25}\\x=\frac{-4}{25}\end{cases}}\)

Vậy \(x=\frac{4}{25}\) hoặc \(x=\frac{-4}{25}\) .

\(c)x^4-16x^2=0\)

\(\Rightarrow x^2\left(x^2-16\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x^2=0\\x^2-16=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x^2=4^2\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=\pm4\end{cases}}\)

Vậy x = 0 hoặc \(x=\pm4\) .