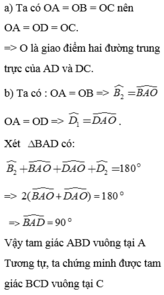Biết điểm C,D cùng nằm trên đường trung trực của AB. Chứng tỏ góc CAD = góc CBD
Những câu hỏi liên quan
16 tháng 7 2015 lúc 14:55
Cho đoạn thẳng AB . Trên đường trung trực D của AB , ta lấy 2 điểm C,D .Biết AD cắt BC tại E và BD cắt AC tại F .
a) C/m góc CAD = góc CBD
B) c/M AF = BE và DF = DE
Cho đoạn thẳng AB và d là đường trung trực của đoạn thẳng AB.Trên đường thẳng d lấy 2 điểm C và D tùy ý.Nối A và B với C và D.
a)Chứng minh góc CAD=góc CBD
b)Gọi E là giao điểm của AC và BD;F là giao điểm của AD và BC.Chứng minh AB//EF
19 tháng 7 2015 lúc 20:22
Cho đoạn thẳng AB . Trên đường trung trực D của AB , ta lấy 2 điểm C,D .Biết AD cắt BC tại E và BD cắt AC tại F .
a) C/m góc CAD = góc CBD
B) c/M AF = BE và DF = DE
18 tháng 7 2015 lúc 7:35
Cho đoạn thẳng AB . Trên đường trung trực D của AB , ta lấy 2 điểm C,D .Biết AD cắt BC tại E và BD cắt AC tại F .
a) C/m góc CAD = góc CBD
B) c/M AF = BE và DF = DE
Giups đi chẳng nhẽ cả onl math không ai giải dk à !!!
Cho tam giác ABC nhọn, O là giao điểm 2 đường trung trực AB và AC, trên tia đối của tia OB lấy điểm D sao cho OB = OD. Chứng minh:
a) O thuộc đường trung trực của AB và CD
b) Chứng minh 2 tam giác ABD và CBD vuông
c) Biết góc ABC = 70 độ. Tính góc ADC
Tam giác ABC nhọn, O là giao điểm hai đường trung trực của AB và AC. Trên tia đối của tia OB lấy điểm D sao cho OB OD.a) Chứng minh O thuộc đường trung trực của AD và CD.b) Chứng minh các tam giác ABD, CBD vuông.c) Biết
A
B
C
^
70
°
. Tính số đo góc
A
D
C
^
.
Đọc tiếp
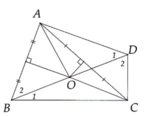
Tam giác ABC nhọn, O là giao điểm hai đường trung trực của AB và AC. Trên tia đối của tia OB lấy điểm D sao cho OB = OD.
a) Chứng minh O thuộc đường trung trực của AD và CD.
b) Chứng minh các tam giác ABD, CBD vuông.
c) Biết A B C ^ = 70 ° . Tính số đo góc A D C ^ .
Cho tam giác ABC nhọn , O là giao điểm hai đường trung trực của AB và AC . Trên tia đối của tia OB lấy điểm D sao cho OB=OD
a, Chứng minh O thuộc đường trung trực của AD và CD
b, Chứng minh các tam giác ABD, CBD vuông
c, Biết góc ABC = 70 độ . Hãy tính số đo góc ADC
Trên đường trung trực của d của đoạn thẳng AB lấy điểm C bất kì.
a) Chứng minh: Tam giác HAC bằng tam giác BBC. Từ đó suy ra CA = CB ( H là giao điểm của D thuộc d )
b) Trên nửa mặt phẳng không chứa điểm C bờ AB lấy điểm D thuộc d. Chứng minh: Tam giác CAD bằng tam giác CBD.
Giải:
Vì d là đường trung trực của AB và cắt AB tại H
\(\Rightarrow AH=HB\) (*)
Xét \(\Delta HAC,\Delta HBC\) có:
AH = HB ( theo (*) )
\(\widehat{AHC}=\widehat{BHC}\left(=90^o\right)\)
CH: cạnh chung
\(\Rightarrow\Delta HAC=\Delta HBC\left(c-g-c\right)\)
\(\Rightarrow CA=CB\) ( hai cạnh tương ứng ) ( đpcm )
b) Vì \(\Delta HAC=\Delta HBC\)
\(\Rightarrow\widehat{C_1}=\widehat{C_2}\) ( góc tương ứng )
Xét \(\Delta CAD,\Delta CBD\) có:
\(CA=CB\)
\(\widehat{C_1}=\widehat{C_2}\)
CD: cạnh chung
\(\Rightarrow\Delta CAD=\Delta CBD\left(c-g-c\right)\)
Đúng 0
Bình luận (0)
Xin lỗi nhé, câu hỏi câu a là thế này:
Chứng minh tam giác HAC bằng tam giác HBC. Từ đó suy ra CA = CB ( H là giao điểm của d với AB)
Đúng 0
Bình luận (0)
Cho C,D cùng nằm trên đường trung trực của AB. Chúng minh góc CAD= góc CBD
https://hoc24.vn/hoi-dap/question/978411.html
Đúng 0
Bình luận (0)