1.Gía trị lớn nhất của hàm số y+x^3-10x^2+25x-4 trên [ 0;5]
2.Hệ{2x-1>=0 và 3x +m<=0 có nghiệm khi nào
3.CHO A,B >0 THỎA A+B<=1 .GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC P+A+B+1/A+/B
4.CHO X>0.HÀM SỐ Y=2X+3/X ĐẠT GIÁ TRỊ NHỎ NHẤT TẠI X
Gía trị lớn nhất của hàm số y = x 5 - 5 x 4 + 5 x 3 + 1 trên đoạn [-1;2] bằng
A. 2
B. 65
C. -7
D. -10
Tìm gía trị nhỏ nhất của hàm số - x + 3 - 1 x + 2 trên nửa khoảng [ - 4 ; - 2 )
A. m i n - 4 ; - 2 y = 4
B. m i n - 4 ; - 2 y = 5
C. m i n - 4 ; - 2 y = 15 2
D. m i n - 4 ; - 2 y = 7
Đáp án là D.
• Ta có: y , = - 1 - 1 ( 2 + x ) 2 cho y , = 0 ⇔ x = - 1 x = - 3
• Bảng biến thiên:
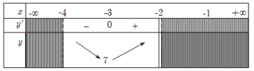
Từ BBT ta có: m i n - 4 ; - 2 y = 7
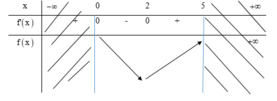
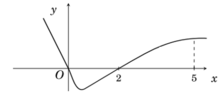
Cho hàm số f (x) có đạo hàm là f ' x . Đồ thị hàm số y = f ' x được cho như hình bên. Biết rằng f 0 + f 3 = f 2 + f 5 . Gía trị nhỏ nhất, giá trị lớn nhất của f (x) trên đoạn 0 ; 5 lần lượt là
A. f 2 , f 5
B. f 0 , f 5
C. f 2 , f 0
D. f 1 , f 5
Đáp án A
Lập được bảng biến thiên của hàm số như sau:
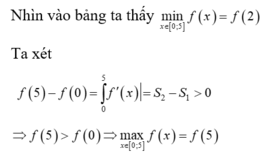
Cho hàm số y=f(x)= -3x^2+10x-4 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×) b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3
Cho bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 4 − 4 x 2 + 3 . Dưới đây là lời giải của học sinh:
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Tính y 0 = 3 ; y − 1 = y 1 = 1 . Vậy giá trị lớn nhất của hàm số là 3, và giá trị nhỏ nhất là 1.
Lời giải trên đúng hay sai? Nếu sai thì giải sai từ bước mấy?
A. Bước 2
B. Lời giải đúng
C. Bước 3
D. Bước 1
Đáp án C
Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .
Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3 trên R
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Ta có bảng biến thiên sau:
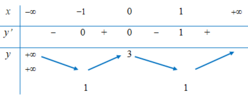
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.
Gía trị lớn nhất của hàm số y = - 2 4 - x là
A. -4
B. -2
C. 1
D. 0
Gía trị lớn nhất của hàm số y = x 3 − 2 x 2 − 4 x + 5 trên đoạn [1;3] bằng
A. -3
B. 0
C. 2
D. 3
Giá trị lớn nhất của hàm số sau trên khoảng (- ∞ ; + ∞ ) là:
y = 1 x 2 + x + 1
A. 1 B. 4/3
C. 5/3 D. 0
1/Giá trị nhỏ nhất của C=(x^2+13)^2
2/Gía trị lớn nhất của B=-(x-3)^2+5/4
3/ Gía trị của x để A=|x-1/3| nhỏ nhất
4/ Tổng các giá trị x thỏa mãn 3x^2-50x=0