Cho tứ diện ABCD có AB ⊥(BCD). Trong tam giác BCD vẽ các đường cao BE và DF cắt nhau tại O. Trong mp(ACD) vẽ DK ⊥AC. Gọi H là trực tâm của tam giác ACD.
a. Chứng minh: (ACD)⊥(ABE) và (ACD)⊥ (DFK).
b. Chứng minh: OH⊥(ACD)
Tứ diện \(ABCD\) có \(AB \bot \left( {BCD} \right)\). Trong tam giác \(BCD\) vẽ đường cao \(BE\) và \(DF\) cắt nhau tại \(O\). Trong mặt phẳng \(\left( {ACD} \right)\) vẽ \({\rm{D}}K\) vuông góc với \(AC\) tại \(K\). Gọi \(H\) là trực tâm của tam giác \(ACD\). Chứng minh rằng:
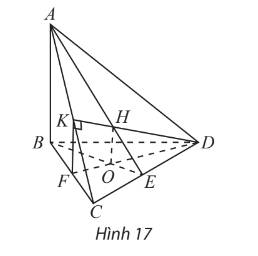
a) \(\left( {ADC} \right) \bot \left( {ABE} \right)\) và \(\left( {ADC} \right) \bot \left( {DFK} \right)\);
b) \(OH \bot \left( {ADC} \right)\).
a) Ta có:
\(\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot C{\rm{D}}\\BE \bot CE\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABE} \right)\)
Lại có \(C{\rm{D}} \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {ABE} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot DF\\DF \bot BC\end{array} \right\} \Rightarrow DF \bot \left( {ABC} \right)\\\left. \begin{array}{l} \Rightarrow DF \bot AC\\DK \bot AC\end{array} \right\} \Rightarrow AC \bot \left( {DFK} \right)\end{array}\)
Lại có \(AC \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {DFK} \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left( {ADC} \right) \bot \left( {ABE} \right)\\\left( {ADC} \right) \bot \left( {DFK} \right)\\\left( {ABE} \right) \cap \left( {DFK} \right) = OH\end{array} \right\} \Rightarrow OH \bot \left( {ADC} \right)\)
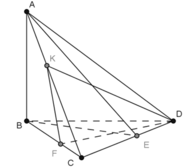
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (BCD). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chứng minh (DFK)⊥(ACD)
- Theo giả thiết:
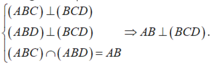
ta có:
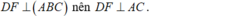
- Vậy ta có:
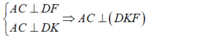
- Lại có:
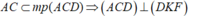
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (BCD). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chứng minh (ABC)⊥(DFK)
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (BCD). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chứng minh (ABE)⊥(ADC)
Cho tứ diện ABCD có AB⊥(BCD). Trong ΔBCD vẽ các đường cao BE và DF cắt nhau ở O. Trong mp(ADC), vẽ DK⊥AC tại K. Chứng minh: (ADC)⊥(DFK)
* Vì: AB ⊥ (BCD) ⇒ AB ⊥ CD.
- Ta có:
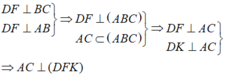
- Lại có:
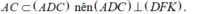
Cho tứ diện ABCD có \(AB \bot (BCD)\), các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của các tam giác BCD, ACD (Hình 31). Chứng minh rằng:
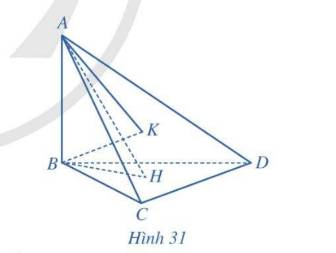
a) \(CD \bot (ABH)\)
b) \(CD \bot (ABK)\)
c) Ba đường thẳng AK, BH, CD cùng đi qua một điểm
a) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có H là trực tâm của tam giác BCD \( \Rightarrow BH \bot CD\left( 2 \right)\)
Tử (1) và (2) \( \Rightarrow CD \bot \left( {ABH} \right)\)
b) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có K là trực tâm của tam giác BCD \( \Rightarrow AK \bot CD\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow CD \bot \left( {ABK} \right)\)
Cho tứ diện ABCD có AB⊥(BCD). Trong ΔBCD vẽ các đường cao BE và DF cắt nhau ở O. Trong mp(ADC), vẽ DK⊥AC tại K. Chứng minh: (ADC)⊥(ABE)
Cho tứ diện ABCD có AB⊥(BCD) . Trong ΔBCD vẽ các đường cao BE và DF cắt nhau ở O. Trong (ADC) vẽ DK⊥AC tại K. Chứng minh: (ADC)⊥(DFK)
Ta có:
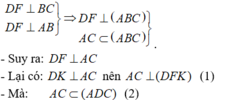
- Từ (1) và (2) suy ra: (ADC) ⊥ (DFK).
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chọn khẳng định sai trong các khẳng định sau?
A. A B E ⊥ A D C
B. A B D ⊥ A D C
C. A B C ⊥ D F K
D. D F K ⊥ A D C