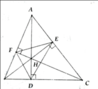
Bài 1: Cho tam giác nhọn ABC có các đường cao AD, BE và CF đồng quy tại H. Chứng minh:
b. H là giao điểm các đường phân giác của
c. BH.BE + CH.CF = BC2
Bài 2: Cho có ba góc nhọn. Gọi O là giao điểm của ba đường cao AH, BK, CI. Chứng minh:
d. BO.BK + CO.CI = BC2