Cho tứ diện ABCD có 2 mặt ABC và DBC là 2 tam giác cân chung đáy BC ,I là trung điểm của BC .CMR:
a) \(BC\perp AC\)
b) \(AH\perp\left(BCD\right)\) .AH là đường cao
Những câu hỏi liên quan
Hai tam giác cân ABC và DBC nằm trong hai mặt phẳng khác nhau có chung cạnh đáy BC tạo nên tứ diện ABCD. Gọi I là trung điểm của cạnh BC
a) Chứng minh \(BC\perp AD\)
b) Gọi AH là đường cao của tam giác ADI
Chứng minh rằng AH vuông góc với mặt phẳng (BCD)
Hai tam giác cân ABC và DBC nằm trong hai mặt phẳng khác nhau có chung cạnh đáy BC tạo nên tứ diện ABCD. Gọi I là trung điểm của cạnh BC.
a) Chứng minh BC ⊥ AD
b) Gọi AH là đường cao của tam giác ADI
Chứng minh rằng AH vuông góc với mặt phẳng (BCD).
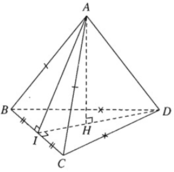
a) Tam giác ABC cân đỉnh A và có I là trung điểm của BC nên AI ⊥ BC. Tương tự tam giác DBC cân đỉnh D và có có I là trung điểm của BC nên DI ⊥ BC. Ta suy ra:
BC ⊥ (AID) nên BC ⊥ AD.
b) Vì BC ⊥ (AID) nên BC ⊥ AH
Mặt khác AH ⊥ ID nên ta suy ra AH vuông góc với mặt phẳng (BCD).
Đúng 1
Bình luận (0)
Cho tứ diện ABCD có hai mặt ABC và BCD là hai tam giác cân có chung đáy BC. Gọi I là trung điểm của cạnh BC.
a) Chứng minh rằng BC vuông góc với mặt phẳng (ADI)
b) Gọi AH là đường cao của tam giác ADI, chứng minh rằng AH vuông góc với mặt phẳng (BCD).
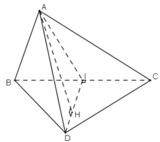
a) Tam giác ABC cân tại A có AI là đường trung tuyến nên đồng thời là đường cao:
AI ⊥ BC
+) Tương tự, tam giác BCD cân tại D có DI là đường trung tuyến nên đồng thời là đường cao:
DI ⊥ BC
+) Ta có: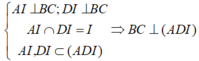 
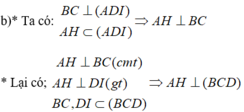
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có hai mặt ABC và BCD là hai tam giác cân có chung cạnh đáy BC. Gọi I là trung điểm của canh BC
a) Chứng minh rằng BC vuông góc với mặt phẳng (ADI)
b) Gọi AH là đường cao của tam giác ADI, chứng minh rằng AH vuông góc với mặt phẳng (BCD)
Cho tam giác ABC vuông tại B ,đường cao AH
a, Cmr \(_{\Delta HBA\sim\Delta HCB\Rightarrow HB^2=HC.HA}\)
b, Kẻ \(HM\perp AB\left(M\in AB\right),HN\perp BC\left(N\in BC\right)\) . Cmr MN=BH
c, Lấy I là trung điểm của HC,K là trung điểm của AH .Tứ giác MNIK là hình gì ?Vì sao?
d, So sánh diện tích tứ giác MNIK và diện tích tam giác ABC
Cho tứ diện ABCD đáy ΔABC cân, DA perp đáy, ABACa, BC dfrac{6}{5}a. M là trung điểm BC. Vẽ AH perpMD. (H thuặc đường thẳng MD)a) C/M AH perp (BCD)b, Cho AD dfrac{4}{3}a. Tính (widehat{AC,DM})c, Gọi G1, G2 lần lượt là các trọng tâm của tam giác ABC và tam giác DBC. CM: G1G2 perp(ABC)
Đọc tiếp
Cho tứ diện ABCD đáy ΔABC cân, DA \(\perp\) đáy, AB=AC=a, BC = \(\dfrac{6}{5}\)a. M là trung điểm BC. Vẽ AH \(\perp\)MD. (H thuặc đường thẳng MD)
a) C/M AH \(\perp\) (BCD)
b, Cho AD = \(\dfrac{4}{3}\)a. Tính (\(\widehat{AC,DM}\))
c, Gọi G1, G2 lần lượt là các trọng tâm của tam giác ABC và tam giác DBC. CM: G1G2 \(\perp\)(ABC)
a: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
mà DA vuông góc (ABC)
nên BC vuông góc (DAM)
=>CB vuông góc AH
mà DM vuông góc AH
nên AH vuông góc (DBC)
b: Kẻ MN//AC(N thuộc AB)
=>(DM;AC)=(DM;MN)=góc DMN hoặc =180 độ-góc DMN
MN=1/2AC=a/2; AN=a/2
DN^2=DA^2+AN^2=89/100a^2
=>AM^2=AB^2-MA^2=a^2-9/25a^2=16/25a^2
=>AM=4/5a
AD=4/5a
=>\(DM=\dfrac{4a\sqrt{2}}{5}\)
DN^2=DM^2+MN^2-2*DM*MN*cosDMN
=>\(\cos DMN=\dfrac{2\sqrt{2}}{5}\)
=>\(\left(AC;DM\right)\simeq56^0\)
c: G1G2//DA
mà DA vuông góc (ABC)
nên G1G2 vuông góc (ABC)
Đúng 1
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:32
Cho tứ diện ABCD có tam giác ABC cân tại \(A\), tam giác BCD cân tại \(D\). Gọi I là trung điểm của cạnh BC.
a) Chứng minh rằng \(BC \bot (AID)\).
b) Kẻ đường cao AH của tam giác AID. Chứng minh rằng \(AH \bot (BCD)\).
c) Kẻ đường cao IJ của tam giác AID. Chứng minh rằng IJ là đường vuông góc chung của AD và BC.
a) Xét tam giác ABC cân tại A có
I là trung điểm của BC
\( \Rightarrow AI \bot BC\)
Xét tam giác ACD cân tại D có
I là trung điểm của BC
\( \Rightarrow DI \bot BC\)
Ta có \(AI \bot BC,DI \bot BC \Rightarrow BC \bot \left( {AID} \right)\)
b) \(BC \bot \left( {AID} \right);BC \subset \left( {BCD} \right) \Rightarrow \left( {BCD} \right) \bot \left( {AID} \right)\)
\(\left( {BCD} \right) \cap \left( {AID} \right) = DI\)
Trong (AID) có \(AH \bot DI\)
\( \Rightarrow AH \bot \left( {BCD} \right)\)
c) Ta có \(BC \bot \left( {AID} \right);IJ \subset \left( {AID} \right) \Rightarrow BC \bot IJ\)
Mà \(IJ \bot AD\)
Do đó IJ là đường vuông góc chung của AD và BC.
Đúng 0
Bình luận (0)
Câu 1 : Cho tam giác ABC đều . Kẻ \(AH\perp BC\left(H\in BC\right)\). TIa phân giác của góc ACB cắt AH tại E . Vẽ \(EK\perp AC\left(K\in AC\right)\). Lấy I là trung điểm của AB . CMR :
a) tam giác EHC = tam giác EKC
b) tam giác CHK đều
c) tam giác AKH cân
d) Ba điểm C,E,I thẳng hàng
Câu 1 : Cho tam giác ABC đều . Kẻ \(AH\perp BC\left(H\in BC\right)\). TIa phân giác của góc ACB cắt AH tại E . Vẽ \(EK\perp AC\left(K\in AC\right)\). Lấy I là trung điểm của AB . CMR :
a) tam giác EHC = tam giác EKC
b) tam giác CHK đều
c) tam giác AKH cân
d) Ba điểm C,E,I thẳng hàng