1−31=−21−31=−2

Với x =4 thì y=x²=4²=16

Với x =-2 thì y=x²=(-2)²=4

Đáp án là B

Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình

1/2 x 2 = (-1)/2 x + 3 ⇔  x 2  + x - 6 = 0

Δ = 1 - 4.1.(-6) = 25 > 0

⇒ Phương trình có 2 nghiệm phân biệt

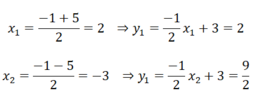
Vậy tọa độ giao điểm của (P) và (d) là (2; 2) và (-3; 9/2)

Phương trình hoành độ giao điểm:

\(-\dfrac{1}{2}x^2=mx+m-3\Leftrightarrow x^2+2mx+2m-6=0\) (1)

a. Khi \(m=-1\), (1) trở thành:

\(x^2-2x-8=0\Rightarrow\left[{}\begin{matrix}x=4\Rightarrow y=-8\\x=-2\Rightarrow y=-2\end{matrix}\right.\)

Vậy (d) cắt (P) tại 2 điểm có tọa độ là \(\left(4;-8\right)\) ; \(\left(-2;-2\right)\)

b. 

\(\Delta'=m^2-2m+6=\left(m+1\right)^2+5>0;\forall m\Rightarrow\left(1\right)\) có 2 nghiệm pb với mọi m

Hay (d) cắt (P) tại 2 điểm pb với mọi m

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=2m-6\end{matrix}\right.\)

\(x_1^2+x_2^2=14\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=14\)

\(\Leftrightarrow4m^2-2\left(2m-6\right)=14\)

\(\Leftrightarrow4m^2-4m-2=0\Rightarrow m=\dfrac{1\pm\sqrt{3}}{2}\)

Hoành độ giao điểm tm pt 

\(x^2-3x+2=0\Leftrightarrow x=1;x=2\)

\(\Rightarrow y=1;y=4\)

Vậy (P) cắt (d) tại A(1;1) ; B(2;4) 

Chọn đáp án A

Phương trình hoành độ giao điểm của (P) và (d) là:

x 2  = 2x - 1 ⇔  x 2  - 2x + 1 = 0 ⇔ x - 1 2  = 0 ⇔ x = 1

Với x = 1 ⇒ y = 1

⇒ Tọa độ giao điểm của (P) và (d) là (1; 1)