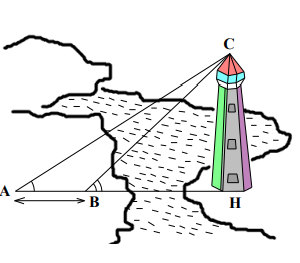
tính CH của biết AB=25, góc HAC=32,HBC=43 và 3 điểm A,B,C thẳng hàng

Những câu hỏi liên quan
tính chiều cao CH của tháp ở bên kia sông, biết AB=25m, góc HAC= 32 °, góc HBC= 43 ° và ba điểm A,B,H thẳng hàng.( làm tròn đến chữ số thập phân thứ nhất ).
mong mọi người giúp ạ :Tính chiều cao CH của tháp ở bên kia sông biết AB = 25cm; 0 0 43 ˆ 32 ; ˆ HAC = HBC = và ba điểm A, B, H thẳng hàng. (kết quả làm tròn đến chữ số thập phân thứ nhất)
Hai xạ thủ đang ở hai vị trí A và B. Họ cần tiêu diệt một tên khủng bố IS đang bắt giữ con tin trên đỉnh ngọn tháp (vị trí C). Biết rằng hai xạ thủ cách nhau 38m và các góc với số đo như sau: HAC 34o ; HBC 52o và ba điểm A, B, H thẳng hàng. Xạ thủ A bắn trước và chỉ trong một phát đạn đã tiêu diệt được mục tiêu. Tính độ dài đường đạn của xạ thủ A (đường đạn bay thẳng, bỏ qua độ quay của Trái đất và sức cản ngang của gió). (Làm tròn hai chữ số thập phân)
Đọc tiếp
Hai xạ thủ đang ở hai vị trí A và B. Họ cần tiêu diệt một tên khủng bố IS đang bắt giữ con tin trên đỉnh ngọn tháp (vị trí C). Biết rằng hai xạ thủ cách nhau 38m và các góc với số đo như sau: HAC = 34o ; HBC = 52o và ba điểm A, B, H thẳng hàng. Xạ thủ A bắn trước và chỉ trong một phát đạn đã tiêu diệt được mục tiêu. Tính độ dài đường đạn của xạ thủ A (đường đạn bay thẳng, bỏ qua độ quay của Trái đất và sức cản ngang của gió). (Làm tròn hai chữ số thập phân)
Cho 3 điểm A B C thẳng hàng B nằm giữa A và C biết BA=2cm BC=3cm. Lấy điểm H bất kì trên đường thẳng vuông góc với AC tại B a) so sánh HB,HA và HC b) giải thích tại sao góc HAC > góc HCA
Xem chi tiết
a: ΔHBA vuông tại B
=>HB<HA
AB<BC
=>HA<HC
=>HB<HA<HC
b: Vì HA<HC
nên góc HAC>góc HCA
Đúng 0
Bình luận (0)
Cho 3 điểm A B C thẳng hàng , B nằm giữa A và C . Biết BA=2cm, BC=3cm. Lấy điểm H bất kì trên đường thẳng vuông góc với AC tại B
a) So sánh HB,HA và HC b) So sánh góc HAC và góc HCAc) So sánh góc BHA và góc BHCa: ΔHBA vuông tại B
=>HB<HA
Vì AB<BC
nên HA<HC
=>HB<HA<HC
b: HA<HC
=>góc HCA<góc HAC
c: HA<HC
=>góc HCA<góc HAC
=>góc AHB>góc BHC
Đúng 0
Bình luận (1)
1. Cho hình thang ABCD có góc A=góc D=90độ. AC⊥Bd tại I. C/m:
a.ABD~DAC
b. Gọi E là hình chiếu của b xuống DC và BO=OD. C/m e điểm O,E,A thẳng hàng
c.Tỉ số diên tích AIB, DIC
2.Cho hình thang cân ABCD có AB//CD, AB<AC, đường chéo BD⊥cạnh bên BC, vẽ đường cao BH
a.BDC~HBC
b.Cho BC=15 cm, DC=25 cm. tính HC,HD
c.diện tích ABCD
Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là \({32^ \circ }\) và \({40^ \circ }\) (Hình 9).

Tam giác ABC vuông tại B nên ta có: \(\tan C = \frac{{AB}}{{CB}} \Leftrightarrow AB = \tan {32^ \circ }.(1 + x)\)
Tam giác ADB vuông tại B nên ta có: \(\tan D = \frac{{AB}}{{DB}} \Leftrightarrow AB = \tan {40^ \circ }.x\)
\(\begin{array}{l} \Rightarrow \tan {32^ \circ }.(1 + x) = \tan {40^ \circ }.x\\ \Leftrightarrow x.(\tan {40^ \circ } - \tan {32^ \circ }) = \tan {32^ \circ }\\ \Leftrightarrow x = \frac{{\tan {{32}^ \circ }}}{{\tan {{40}^ \circ } - \tan {{32}^ \circ }}}\\ \Leftrightarrow x \approx 2,9\;(km)\end{array}\)
\( \Rightarrow AB \approx \tan {40^ \circ }.2,92 \approx 2,45\;(km)\)
Vậy chiều cao của ngọn núi là 2,45 km.
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB//CD)
a,Biết góc A: góc B: góc C =6:5:4.Tính góc a ,góc b , góc c , góc d?
b,Biết rằng AD+BC=AB.Hai tia phân giác của góc C và góc D cắt nhau tại E .CMR: 3 điểm A,E,B thẳng hàng
Cho ba điểm A,B,C thẳng hàng,B nằm giữa A và C biết BA=2cm,BC=3cm.Lấy điểm H bất kỳ trên đường thẳng vuông góc với AC tại B
a)So sánh HB,HA và HC
b)So sánh HAC và HCA
c)So sánh BHA và BHC
vẽ hình giúp mình nữa nhé!
a: Xet ΔHAC có AB<BC
mà AB,BC lần lượt là hình chiếu của HA,HC trên AC
nên HA<HC
mà HB<HA
nên HB<HA<HC
b: HA<HC
=>góc HCA<góc HAC
c: góc HCA<góc HAC
=>90 độ-góc HCA>90 độ-góc HAC
=>góc BHC>góc BHA
Đúng 3
Bình luận (0)




 Hình
Hình









