Cho tam giác ABC có đường phân giác BE và CF. Trên đoạn EF lấy M bất kì. Gọi I,K,H lần lượt là chân đường buông góc hạ từ M xuống AB,AC và BC. Cm MH=MK+MI

Những câu hỏi liên quan
Cho tam giác ABC có
B
A
C
⏜
60
0
,
A
C
b
,
A
B
c
b
c
. Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc...
Đọc tiếp
Cho tam giác ABC có B A C ⏜ = 60 0 , A C = b , A B = c b > c . Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc với BC tại M (E thuộc cung lớn BC). Gọi I và J là chân đường vuông góc hạ từ E xuống các đường thẳng AB và AC. Gọi H và K là chân đường vuông góc hạ từ F xuống các đường thẳng AB và AC.
b) Chứng minh I, J, M thẳng hàng và IJ vuông góc với HK.
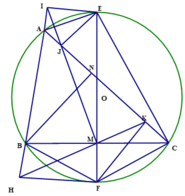
b) Ta có I E M ⏜ = A E C ⏜ ⇒ A E I ⏜ = C E M ⏜ .
Mặt khác A E I ⏜ = A J I ⏜ ( cùng chắn cung IJ), C E M ⏜ = C J M ⏜ ( cùng chắn cung CM). Suy ra C J M ⏜ = A J I ⏜ . Mà I, M nằm hai phía của đường thẳng AC nên C J M ⏜ = A J I ⏜ đối đỉnh suy ra I, J, M thẳng hàng.
Tương tự, ta chứng minh được H, M, K thẳng hàng.
Do tứ giác CFMK nội tiếp nên C F K ⏜ = C M K ⏜ .
Do tứ giác CMJE nội tiếp nên J M E ⏜ = J C E ⏜ .
Mặt khác E C F ⏜ = 90 0 ⇒ C F K ⏜ = J C E ⏜ ( vì cùng phụ với A C F ⏜ ).
Do đó C M K ⏜ = J M E ⏜ ⇒ J M K ⏜ = E M C ⏜ = 90 0 hay I J ⊥ H K
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có 2 đường phân giác BE,CF.
1) CMR: Tam giác AEF là tam giác có 3 góc nhọn
2) Gọi M là điểm thuộc EF. Gọi K,H,Q lần lượt là hình chiếu của M trên AB,AC,BC. CMR: MQ = MK + MH
Cho tam giác ABC có 3 góc nhọn. Kẻ 2 đường cao BE và CF
a. biết góc BAC = \(60^o\) Tính EF theo BC=a
b. Trên nửa đường tròn đường kính BC không chứa E và F lấy 1 điểm M bất kì. gọi H,I,K lần lượt là hình chiếu vuông góc của M trên BC,CE,EB. Tìm GTNN của \(S=\frac{BC}{MH}+\frac{CE}{MI}+\frac{EB}{MK}\)
Cho tam giác ABC có
B
A
C
⏜
60
0
,
A
C
b
,
A
B
c
b
c
. Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc...
Đọc tiếp
Cho tam giác ABC có B A C ⏜ = 60 0 , A C = b , A B = c b > c . Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc với BC tại M (E thuộc cung lớn BC). Gọi I và J là chân đường vuông góc hạ từ E xuống các đường thẳng AB và AC. Gọi H và K là chân đường vuông góc hạ từ F xuống các đường thẳng AB và AC.
c) Tính độ dài cạnh BC và bán kính đường tròn ngoại tiếp tam giác ABC theo b, c.

c)
K ẻ B N ⊥ A C N ∈ A C . B A C ⏜ = 60 0 ⇒ A B N ⏜ = 30 0 ⇒ A N = A B 2 = c 2 ⇒ B N 2 = A B 2 − A N 2 = 3 c 2 4 ⇒ B C 2 = B N 2 + C N 2 = 3 c 2 4 + b − c 2 2 = b 2 + c 2 − b c ⇒ B C = b 2 + c 2 − b c
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác ABC. Xét tam giác đều BCE có R = O E = 2 3 E M = 2 B C 3 3.2 = 1 3 . 3 b 2 + c 2 − b c
Đúng 0
Bình luận (0)
Cho tam giác ABC có giao điểm các đường phân giác tại I. D E F lần lượt là chân đường vuông góc hạ từ I xuống BC,CA và AB. Hạ DH vuông góc với EF biết H thuộc EF. Cm HD là đường phân giác góc BHC
cho tam giác ABC có ba góc nhọn,các đường cao AD,BE,CF cắt nhau tại H
A , cm tam giác BDA đồng dạng tam giác BFC
B, cm tam giác AEF đồng dạng ABC
C, cm AH.AD+CH.CF=AC^2
D, Gọi M,N,P,Q lần lượt là chân các đường vuông óc hạ từ D xuống AB,BE,CF,AC cm bốn điểm M,N,P,Q cùng nằm trên một đường thẳng
MỌI NGƯỜI GIÚP MK VỚI TẠI MK CẦN CÁI NÀY GẤP Ạ
a: Xét ΔBDA vuông tại D và ΔBFC vuông tại F co
góc B chung
=>ΔBDA đồng dạng vói ΔBFC
b: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc AFE=góc ACB
=>ΔAFE đồng dạng vói ΔACB
c: Xét ΔAEH vuông tại E và ΔADC vuông tại D có
góc EAH chung
=>ΔAEH đồng dạng vói ΔADC
=>AD*AH=AE*AC
Xét ΔCEH vuông tại E và ΔCFA vuông tại F có
góc ECH chung
=>ΔCEH đồng dạng vói ΔCFA
=>CH*CF=CE*CA
=>AH*AD+CH*CF=CA^2
Đúng 0
Bình luận (0)
Cho tam giác ABC có 2 đường phân giác BD và CE (D thuộc AC, E thuộc AB). Trên ED lấy điểm M bất kì, lấy L,K,H lần lượt thuộc AB,AC,BC sao cho MH ⊥ BC, ML ⊥ AB, MK ⊥ AC. chứng minh MH = ML + MK
Cho tam giác ABC có
B
A
C
⏜
60
0
,
A
C
b
,
A
B
c
b
c
. Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc...
Đọc tiếp
Cho tam giác ABC có B A C ⏜ = 60 0 , A C = b , A B = c b > c . Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc với BC tại M (E thuộc cung lớn BC). Gọi I và J là chân đường vuông góc hạ từ E xuống các đường thẳng AB và AC. Gọi H và K là chân đường vuông góc hạ từ F xuống các đường thẳng AB và AC.
a) Chứng minh các tứ giác AIEJ, CMJE nội tiếp và E A . E M = E C . E I .
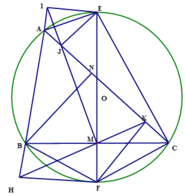
a) Ta có: A I E ^ = A J E ^ = 90 0 nên tứ giác AIEJ nội tiếp.
E M C ^ = E J C ^ = 90 0 nên tứ giác CMJE nội tiếp.
Xét tam giác Δ A E C v à Δ I E M , có
A C E ⏜ = E M I ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác CMJE).
E A C ⏜ = E I M ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác AIEJ).
Do đó hai tam giác Δ A E C ~ Δ I E M đồng dạng
⇒ A E E I = E C E M ⇒ E A . E M = E C . E I (đpcm)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A. M là trung điểm BC, trên tia đối của MA lấy điểm D sao cho AMMD. gọi I và K lần lượt là chân đường vuông góc hạ từ B và C xuống AD, N là chân đường vuông góc hạ từ M xuống ACa)CMR BKCI và BK song song CIb)CM KNMCc)tam giác ABC thoả mãn điều kiện gì để AIIMMKKDd)gọi H là chân đường vuông góc hạ từ D xuống BC. CM các đường thẳng BI,DH,MN đồng quy
Đọc tiếp
cho tam giác ABC vuông tại A. M là trung điểm BC, trên tia đối của MA lấy điểm D sao cho AM=MD. gọi I và K lần lượt là chân đường vuông góc hạ từ B và C xuống AD, N là chân đường vuông góc hạ từ M xuống AC
a)CMR BK=CI và BK song song CI
b)CM KN<MC
c)tam giác ABC thoả mãn điều kiện gì để AI=IM=MK=KD
d)gọi H là chân đường vuông góc hạ từ D xuống BC. CM các đường thẳng BI,DH,MN đồng quy










