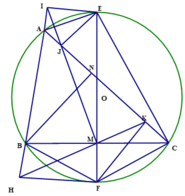
Cho tam giác ABC có B A C ⏜ = 60 0 , A C = b , A B = c b > c . Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc với BC tại M (E thuộc cung lớn BC). Gọi I và J là chân đường vuông góc hạ từ E xuống các đường thẳng AB và AC. Gọi H và K là chân đường vuông góc hạ từ F xuống các đường thẳng AB và AC.
b) Chứng minh I, J, M thẳng hàng và IJ vuông góc với HK.
b) Ta có I E M ⏜ = A E C ⏜ ⇒ A E I ⏜ = C E M ⏜ .
Mặt khác A E I ⏜ = A J I ⏜ ( cùng chắn cung IJ), C E M ⏜ = C J M ⏜ ( cùng chắn cung CM). Suy ra C J M ⏜ = A J I ⏜ . Mà I, M nằm hai phía của đường thẳng AC nên C J M ⏜ = A J I ⏜ đối đỉnh suy ra I, J, M thẳng hàng.
Tương tự, ta chứng minh được H, M, K thẳng hàng.
Do tứ giác CFMK nội tiếp nên C F K ⏜ = C M K ⏜ .
Do tứ giác CMJE nội tiếp nên J M E ⏜ = J C E ⏜ .
Mặt khác E C F ⏜ = 90 0 ⇒ C F K ⏜ = J C E ⏜ ( vì cùng phụ với A C F ⏜ ).
Do đó C M K ⏜ = J M E ⏜ ⇒ J M K ⏜ = E M C ⏜ = 90 0 hay I J ⊥ H K










