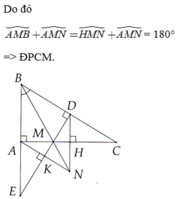
Cho tam giác ABC vuông tại A,tia phân giác góc B cắt cạnh AC tại M.Kẻ MD vuông góc với BC tại D.
a)Chứng minh: góc BMA = góc BMD
b)Gọi E là giao điểm của hai đường thẳng MD và BA Chứng minh:AC=DE
c)Chứng minh: Δ A M E = Δ D M C
d)Kẻ DH ⊥ MC tại H và AK ⊥ ME tại K.Hai tia DH và AK cắt nhau tại N.Chứng minh:MN là phân giác của góc KMH
e)Chứng minh:Ba điểm B,M,N thẳng hàng g)Chứng minh:BN ⊥ AD,BN ⊥ EC
h) Δ ABC thỏa mãn điều kiện gì để Δ NAD là tam giác đều