cho hình bình hành abcd gọi e là trung điểm của ab ,f là trung điểm của cd. cmr de=bf
Cho hình bình hành ABCD. Gọi E là trung điểm của AB, F là trung điểm của CD. Chứng minh rằng: DE = BF
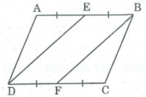
Ta có: AB = CD (tính chất hình bình hành)
EB = 1/2 AB (gt)
FD = 1/2 CD (gt)
Suy ra: EB = FD (1)
Mà AB // CD (gt)
⇒ BE // FD (2)
Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ DE = BF (tính chất hình bình hành)
Cho hình bình hành ABCD. Gọi E là trung điểm của AB, F là trung điểm của CD. Chứng minh rằng: DE = BF
Giải:
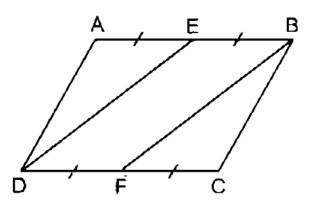
Ta có: AB = CD ( tính chất hình bình hành)
\(EB=\frac{1}{2}AB\left(gt\right)\)
\(FD=\frac{1}{2}CD\left(gt\right)\)
Suy ra: EB = FB (1)
Mà AB // CD (gt)
⇒ BE // FD (2)
Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ DE = BF (tính chất hình bình hành)
Ta có: AB = CD (tính chất hình bình hành)
EB = 1/2 AB (gt)
FD = 1/2 CD (gt)
Suy ra: EB = FD (1)
Mà AB // CD (gt)
⇒ BE // FD (2)
Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ DE = BF (tính chất hình bình hành)
Cho tứ giác ABCD . Gọi E và F là trung điểm của AB và CD . Gọi M,N,P,Q là trung điểm DE,BF,CE,AF . CMR: MNPQ là Hình bình hành
cach lam moi la
Cho hình bình hành ABCD. Gọi E là trung điểm của AB, F là trung điểm của CD. Chứng minh rằng: DE = BF
Ta có \(EB=\dfrac{1}{2}AB\left(E.là.trung.điểm.AB\right)\)
\(FD=\dfrac{1}{2}CD\left(F.là.trung.điểm.CD\right)\)
\(AB=CD\left(hbh.ABCD\right)\Rightarrow\dfrac{1}{2}AB=\dfrac{1}{2}CD\)
\(\Rightarrow BE=DF;BE//DF\left(AB//CD\right)\)
Do đó BEDF là hbg
\(\Rightarrow DE=BF\)
Cho hình bình hành ABCD, gọi E là trung điểm của AB ,F là trung điểm của CD .khi đó
A. DE=BF B. DE > BF C. DE < BF D. DE=EB
trắc nghiệm nha mn lm giúp mik với mai kt r
Cho hình bình hành ABCD. Gọi E là trung điểm của AB, F là trung điểm của CD.
Chứng minh rằng DE = BF ?
Hình bình hành:
1. Cho tứ giác ABC, gọi E, F là trung điểm của AB và CD; M, N, P, Q lần lượt là trung điểm các đoạn AF, CE, BF và DE. C Chứng minh rằng MNPQ là hình bình hành.
2. Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho AE = EF = FC. Gọi M là giao điểm của BF và CD; N là giao điểm của DE và AB. Chứng minh rằng:
a. M, N theo thứ tự là trung điểm của CD, AB.
b. EMFN là hình bình hành.
Cho hình bình hành ABCD có AB = 2AD. Gọi E là trung điểm AD, F là trung điểm CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. AECF là hình bình hành, AEDF là hình bình hành. Chứng minh rằng MN = EF
Ai giúp e vs ạ 8h30 e phải nộp rùi please
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
cho hình bình hành ABCD gọi E,F theo thứ tự là trung điểm của AB,CD Gọi M là giao điểm của AF và DE, N là giao điểm BF và CE
a) CMR EMFN là hình bình hành
b) Các Đường thẳng AC, EF, MN Đồng quy