Cho tam giác AOB trên tia đối của tia OA lấy điểm C trên tia đối của tia OB lấy điểm C c/m ab//cd

Những câu hỏi liên quan
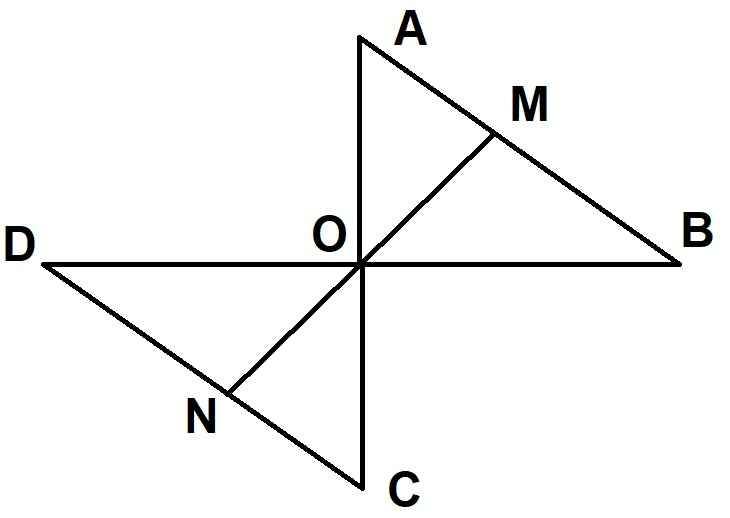
Cho tam giác AOB. Trên tia đối của tia OA lấy điểm C sao cho OC = OA , trên tia đối của tia OB lấy điểm D sao cho OD = OB
1, chứng ming : ∆AOB = ∆COD
2, gọi M là điểm nằm giữa A và B . Tia MO cắt CD tại N . Chứng minh rằng MB = ND
3,Trên tia AB lấy M , trên tia DC lấy N sao cho BM=DN . CMR: M,O,N thẳng hàng
a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)
Đúng 1
Bình luận (0)
a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)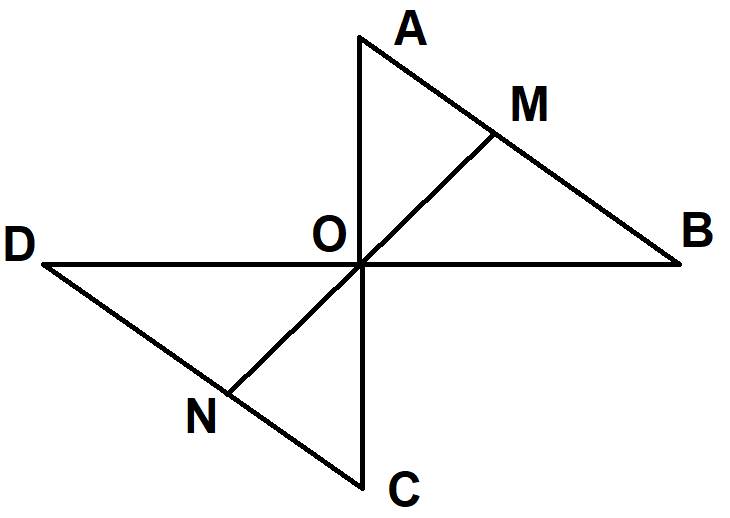
Đúng 0
Bình luận (0)
a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)
Đúng 0
Bình luận (0)
Cho tam giác AOB. Trên tia đối của tia OA lấy điểm C sao cho OC = OA, trên tia đối của tia OB lấy điểm D sao cho OD = OB
a) Chứng minh CD // AB
b)Gọi M là một điểm nằm giữa A và B. Tia MO cắt CD ở N. Chứng minh MA=NC
 có đẹp không ạ
có đẹp không ạ 
Bài 8: Cho tam giác AOB . Trên tia đối của tia OA lấy điểm C sao cho OC = OA. Trên tia đối của tia OB lấy điểm D sao cho OD = OB.
a) Chứng minh : ∆OAB = ∆OCD b) Chứng minh : AB// CD
Gọi M là một điểm nằm giữa A và B . Tia MO cắt cạnh CD ở N . Chứng minh OM = ON
Mọi người giúp mình với ạ! Mình đang cần gấp :))
b: Xét tứ giác ABCD có
O là trung điểm của AC
O là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD
Đúng 0
Bình luận (0)
Cho tam giác AOB. Trên tia đối của tia OA lấy điểm C sao cho OC = OA, trên tia đối của tia OB lấy điểm D sao cho OD = OB
a/ Chứng minh AB // CD
b/ M là nột điểm nằm giữa A và B. Tia MO cắt CD ở N. Chứng minh :△OAM =△ONC
c/ Từ M kẻ MI vuông góc với OA , từ N kẻ NF vuông góc OC. Chứng minh : MI = NF
a: Xét tứ giác ABCD có
O là trung điểm của AC
O là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD
Đúng 0
Bình luận (0)
Cho tam giác AOB. Trên tia đối của tia OA lấy điểm C sao cho OC = OA, trên tia đối của tia OB lấy điểm D sao cho OD = OB
a) Chứng minh AB // CD
b) M là 1 điểm nằm giữa A và B. Tia MO cắt CD ở N, chứng minh: tam giác OAM = tam giác ONC
c) Từ M kẻ MI vuông góc với OA, từ N kẻ NF vuông góc OC, chứng minh: MI = MF
Cho tam giác ABO. Trên Tia đối của tia OA lấy điểm C sao cho OA=OC. Trên tia đối của tia OB lấy điểm D sao cho OB=OD.
a, CM: tam giác ABO = tam giác CDO
b, CM: AB//CD
c, lấy điểm M,N lần lượt là trung điểm của AB và CD. Chứng minh rằng ba điểm M,O,N thẳng hàng.
a) Xét tam giác tam giác ABO và tam giác CDO có:
+ OB = OD (gt).
+ OA = OC (gt).
+ ^AOB = ^COD (2 góc đối đỉnh).
=> Tam giác ABO = Tam giác CDO (c - g - c).
b) Xét tứ giác ABCD có:
+ O là trung điểm của AC (do OA = OC).
+ O là trung điểm của BD (do OB = OD).
=> Tứ giác ABCD là hình bình hành (dhnb).
=> AB // CD (Tính chất hình bình hành).
c) Xét tam giác ABC có:
+ M là trung điểm của AB (gt).
+ O là trung điểm của AC (do OA = OC).
=> MO là đường trung bình.
=> MO // BC (Tính chất đường trung bình trong tam giác). (1)
Xét tam giác BDC có:
+ N là trung điểm của CD (gt).
+ O là trung điểm của BD (do OB = OD).
=> NO là đường trung bình.
=> NO // BC (Tính chất đường trung bình trong tam giác). (2)
Từ (1) và (2) => 3 điểm M; O; N thẳng hàng (đpcm).
Đúng 0
Bình luận (0)
Cho tam giác ABO. Trên Tia đối của tia OA lấy điểm C sao cho OA=OC. Trên tia đối của tia OB lấy điểm D sao cho OB=OD.
a, CM: tam giác ABO = tam giác CDO
b, CM: AB//CD
c, lấy điểm M,N lần lượt là trung điểm của AB và CD. Chứng minh rằng O là trung điểm của MN.
a) Xét tam giác tam giác ABO và tam giác CDO có:
+ \(\text{OB = OD}\) (gt).
+ \(\text{OA = OC }\)(gt).
+ \(\widehat{AOB}\) = \(\widehat{COD}\) (2 góc đối đỉnh).
=> Tam giác ABO = Tam giác CDO (c - g - c).
b) Xét tứ giác ABCD có:
+ O là trung điểm của AC (do \(\text{OA = OC}\)).
+ O là trung điểm của BD (do \(\text{OB = OD}\)).
=> Tứ giác ABCD là hình bình hành (dhnb).
=> AB // CD (Tính chất hình bình hành).
c) Xét tam giác ABC có:
+ M là trung điểm của AB (gt).
+ O là trung điểm của AC (do \(\text{OA = OC}\)).
=> MO là đường trung bình.
=> MO // BC và MO = \(\dfrac{1}{2}\) BC (Tính chất đường trung bình trong tam giác). (1)
Xét tam giác BDC có:
+ N là trung điểm của CD (gt).
+ O là trung điểm của BD (do \(\text{OB = OD}\)).
=> NO là đường trung bình.
=> NO // BC và NO = \(\dfrac{1}{2}\) BC (Tính chất đường trung bình trong tam giác). (2)
Từ (1) và (2) => 3 điểm M; O; N thẳng hàng và MO = NO (do cùng = \(\dfrac{1}{2}\) BC).
=> O là trung điểm của MN (đpcm).
Đúng 0
Bình luận (0)
a) Xét tam giác tam giác ABO và tam giác CDO có:
+ OB = ODOB = OD (gt).
+ OA = OC OA = OC (gt).
+ ˆAOB���^ = ˆCOD���^ (2 góc đối đỉnh).
=> Tam giác ABO = Tam giác CDO (c - g - c).
b) Xét tứ giác ABCD có:
+ O là trung điểm của AC (do OA = OCOA = OC).
+ O là trung điểm của BD (do OB = ODOB = OD).
=> Tứ giác ABCD là hình bình hành (dhnb).
=> AB // CD (Tính chất hình bình hành).
c) Xét tam giác ABC có:
+ M là trung điểm của AB (gt).
+ O là trung điểm của AC (do OA = OCOA = OC).
=> MO là đường trung bình.
=> MO // BC và MO = 1212 BC (Tính chất đường trung bình trong tam giác). (2)
Từ (1) và (2) => 3 điểm M; O; N thẳng hàng và MO = NO (do cùng =
Đúng 0
Bình luận (0)
Cho tam giác AOB. Trên tia đối của tia OA lấy điểm C sao cho OC = OA , trên tia đối của tia OB lấy điểm D sao cho OD = OB
a) Chứng minh AB // CD
b) M là một điểm nằm giữa A và B. Tia MO cắt CD ở N, CMR: OM = ON
c) Từ M kẻ MI vuông góc với OA , từ N kẻ NF vuông góc OC. CMR: MI = NF
Cho tam giác AOB . Trên tia đối của tia OA lấy điểm C sao cho OC = OA. Trên tia đối của tia OB sao cho OD = OB.
a) Chứng minh : ∆OAB = ∆OCD b) Chứng minh : AB// CD
b) Gọi M là một điểm nằm giữa A và B . Tia MO cắt cạnh CD ở N . Chứng minh OM = ON
giúp mình cần gấp lắm ạ
b: Xét tứ giác ABCD có
O là trung điểm của AC
O là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD
Đúng 0
Bình luận (0)

















