cho AM , BN là hai trung tuyến của tam giác ABC . Hãy phân tích véc tơ BC
theo hai vec tơ AM và BN
Cho tam giác ABC và M là trung điểm BC. Phân tích vec tơ AM theo vec tơ BA và vec tơ CA
Cho tam giác ABC có 3 trung tuyến AM,BN,CK và trọng tâm G. Chứng minh:
a/véc tơ AM + véc tơ BN + véc tơ CK = véc tơ 0 ( đã xong )
b/ véc tơ GM + véc tơ GN + véc tơ GK = véc tơ 0 ( đã xong )
c/ 3.véc tơ AG = 2.(véc tơ AK + véc tơ AN )
Làm giúp mình câu c thôi ạ :(
Theo tính chất trọng tâm ta có: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
Mặt khác AM là trung tuyến nên: \(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)\Rightarrow3\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{AC}\) (1)
K là trung điểm AB, N là trung điểm AC nên: \(\left\{{}\begin{matrix}\overrightarrow{AK}=\dfrac{1}{2}\overrightarrow{AB}\\\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=2\overrightarrow{AK}\\\overrightarrow{AC}=2\overrightarrow{AN}\end{matrix}\right.\) (2)
(1);(2) \(\Rightarrow3\overrightarrow{AG}=2\left(\overrightarrow{AK}+\overrightarrow{AN}\right)\)
Cho AK và BM là hai trung tuyến của tam giác ABC. Hãy phân tích các vectơ 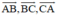 theo hai vec tơ
theo hai vec tơ 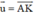 và
và 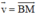
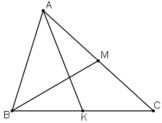
+ K là trung điểm của BC nên ta có:
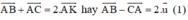
+ M là trung điểm AC nên ta có:
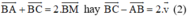
+ Lại có 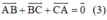
Cộng (1) với (3) ta được 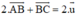 ,
,
kết hợp với (2) ta được hệ phương trình: 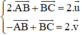
Giải hệ phương trình ta được
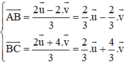
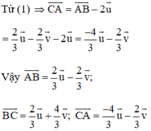
Lời giải:
Ta có:
\(\overrightarrow{AB}=\overrightarrow{AM}+\overrightarrow{MB}=\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NB}=\overrightarrow{AM}-\overrightarrow{BN}+\overrightarrow{MN}\)
Vì $AM,BN$ là trung tuyến nên $M,N$ lần lượt là trung điểm của $BC, AC$
$\Rightarrow MN$ là đường trung bình của tam giác $ABC$ ứng với $AB$
\(\Rightarrow \overrightarrow{MN}=\frac{1}{2}\overrightarrow{BA}=-\frac{1}{2}\overrightarrow{AB}\). Do đó:
\(\overrightarrow{AB}=\overrightarrow{AM}-\overrightarrow{BN}-\frac{1}{2}\overrightarrow{AB}\Leftrightarrow \frac{3}{2}\overrightarrow{AB}=\overrightarrow{AM}-\overrightarrow{BN}\)
\(\Leftrightarrow \overrightarrow{AB}=\frac{2}{3}\overrightarrow{AM}-\frac{2}{3}\overrightarrow{BN}\)
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho 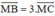 . Hãy phân tích vec tơ
. Hãy phân tích vec tơ 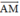 theo hai vec tơ
theo hai vec tơ 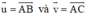
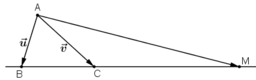
Ta có: 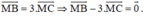
Theo quy tắc ba điểm ta có:
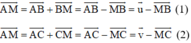
Lấy (1) trừ 3 lần (2) ta được:
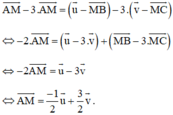
Cho tam giác ABC .Gọi M , N, P lần lượt là trung điểm của BC , CA , AB và O là điểm bất kì .CMR
a, tổng các véc tơ AM +BN + CP bằng véc tơ 0
b, OA +OB+ OC = OM + ON +OP
Cho hình bình hành ABCD. Gọi N là trung điểm cạnh CD. Trên cạnh AC lấy điểm M sao cho AM = 2MC; Phân tích các vec tơ sau theo hai véc tơ ABvà AD
a. vecto ac
b) vecto AM
c) vecto an
Lời giải:
a.
$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$ (tính chất hình bình hành)
b.
$\overrightarrow{AM}=\frac{2}{3}\overrightarrow{AC}=\frac{2}{3}(\overrightarrow{AB}+\overrightarrow{AD})$
c.
$\overrightarrow{AN}=\overrightarrow{AC}+\overrightarrow{CN}=\overrightarrow{AC}+\frac{1}{2}\overrightarrow{BA}$
$=\overrightarrow{AB}+\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$
$=\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}$
Tam giác ABC có hai trung tuyến AM và BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo hai cạnh AM và BN
A. S A B C = A M . B N
B. S A B C = 3 2 A M . B N
C. S A B C = 1 2 A M . B N
D. S A B C = 2 3 A M . B N
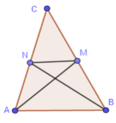
Ta có ABMN là tứ giác có hai đường chéo AM và BN vuông góc
nên có diện tích là: SABMN = 1 2 AB.MN
Hai tam giác AMC và ABC có chung đường cao hạ từ A
nên S A M C S A B C = M C B C = 1 2
=> SAMC = 1 2 SABC (1)
Hai tam giác AMN và AMC có chung đường cao hạ từ M
nên S A M N S A M C = A N A C = 1 2
=> SAMB = 1 2 SABC (2)
Từ (1) và (2) suy ra SAMN = 1 4 SABC
Hai tam giác AMB và ABC có chung đường cao hạ từ A
nên S A M B S A B C = B M B C = 1 2
=> SAMB = 1 2 SABC
Ta có: SABMN = SAMN + SABM
= 1 4 SABC + 1 2 SABC = 3 4 SABC
=> SABC = 4 3 SABMN = 4 3 .AM. 1 2 BN = 2 3 AM.BN
Đáp án cần chọn là: D
Tam giác ABC có hai trung tuyến AM, BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo AM và BN.
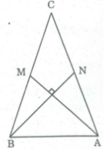
Tứ giác ẠBMN có hai đường chéo vuông góc.
Ta có: S A B M N = 1/2 AM.BN
∆ ABM và ∆ AMC có chung chiều cao kể từ A, cạnh đáy BM = MC nên: S A B M = S A M C = 1/2 S A B C
∆ MNA và ∆ MNC có chung chiều cao kê từ M, cạnh đáy AN = NC nên: S M A N = S M N C = 1/2 S A M C = 1/4 S A B C
S A B M N = S A B M + S M N A = 1/2 S A B C + 1/4 S A B C = 3/4 S A B C
Vậy S A B C = 4/3 S A B M N = 4/3 .1/2 .AM.BN = 2/3 AM.BN