Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H\(\subset\)BC). Chứng minh:
a) \(\Delta ABH=\Delta ACH\)
b) AH là tia phân giác của góc BAC
Cho tam giác ABC cân tại A có AB = 10cm, BH = 6cm. Vẽ AH vuông góc BC tại H.
a, Tính AH =?
b) Chứng minh tam giác ABH= tam giác ACH , từ đó chứng minh AH là tia phân giác của góc A.
c) Từ H vẽ HM vuông góc AB (M ϵ AB) và kẻ HN vuông góc AC (N ϵ AC) .
Chứng minh : tam giác BHM = tam giác HCN
d) Từ B kẻ Bx vuông góc AB, từ C kẻ Cy vuông góc AC chúng cắt nhau tại O. Tam giác OBC là tam giác gì? Vì sao?
CÁC BẠN VẼ HÌNH GIÚP MÌNH NHA! MÌNH CẢM ƠN CÁC BẠN! ![]()
a: Ta có: ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=10^2-6^2=64\)
=>\(AH=\sqrt{64}=8\left(cm\right)\)
b: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
c: Ta có: ΔAHB=ΔAHC
=>BH=CH
Xét ΔBMH vuông tại M và ΔCNH vuông tại N có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔBMH=ΔCNH
d: Xét ΔABO vuông tại B và ΔACO vuông tại C có
AO chung
AB=AC
Do đó: ΔABO=ΔACO
=>OB=OC
=>ΔOBC cân tại O
Bài tập 2: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (HÎBC). Chứng minh:
∆ABH = ∆ACH
a) AH là tia phân giác của góc BAC.
a) Xét \(\Delta ABH\)và \(\Delta ACH\)có:
\(AB=AC\left(gt\right)\)
\(\widehat{AHB}=\widehat{AHC}\left(=90^0\right)\)
AH là cạnh chung
\(\Rightarrow\Delta ABH=\Delta ACH\left(ch.gn\right)\)
a) Vì \(\Delta ABH=\Delta ACH\left(cmt\right)\)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\)( 2 cạnh tương ứng )
=> AH là tia phân giác \(\widehat{BAC}\left(đpcm\right)\)
a:Xét tam giác ABH vuông tại H và tam giác ACH vuông tại H có
AH chung
AC =AB (giả thiết)
Suy ra tam giác ABH = tam giác ACH ( cạnh huyền cạnh góc vuông)
b:từ trên suy ra : góc CAH = góc BAH
Suy ra AH là tia phân giác của góc BAC
Vì \(\Delta ABC\) cân tại A nên \(AB=AC\) ; \(\widehat{B}\)= \(\widehat{C}\)
Xét \(\Delta ABH\)và \(\Delta ACH\)có: \(AB=AC\)
\(\widehat{B}=\widehat{C}\)
\(\widehat{AHB}=\widehat{AHC}=90\)độ
\(\Rightarrow\)\(\Delta AHB=\Delta AHC\left(ch-gn\right)\)
a)Vì \(\Delta AHB=\Delta AHC\)nên \(\widehat{BAH}=\widehat{CAH}\)
\(\Rightarrow\)AH là tia phân giác góc BAC
Cho tam giác ABC có AB= AC. Gọi H là trung điểm BC a) chứng minh tam giác ABH = tam giác ACH b) chứng minh AH vuông góc BC c) AH là tia phân giác góc BAC
a: Xét ΔABH và ΔACH có
AB=AC
AH chung
HB=HC
Do đó: ΔAHB=ΔAHC
a: Xét ΔABH và ΔACH có
AB=AC
AH chung
HB=HC
➩ ΔAHB=ΔAHC (c-c-c)
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H
a/ Chứng minh :tam giác AHB = tam giác AHCvà AH là tia phân giác của góc BAC
b/ Từ H kẻ HM vuông góc với AB, HN vuông góc với AC ,AH cắt MN tại K. Chứng minh AH vuông góc với MN
c/ Trên tia đối của tia HM lấy P sao cho H là trung điểm của MP, NP cắt BC tại E, NH cắt ME tại Q. Chứng minh: P, Q, K thẳng hàng.
\(\Delta ABC\)cân tại A, tia phân giác Ax cắt BC tại H (H∈BC)
a) Chứng minh \(\Delta ABH\)= \(\Delta ACH\)
b) Chứng minh AH vuông góc với BC
c) Cho AB = 6cm; BC = 7cm. Tính AH
giải
a, Xét \(\Delta ABH\)và \(\Delta ACH\)có :
\(\widehat{ABH}=\widehat{ACH}\)( Vì tam giác ABC cân tại A )
\(AH\)chung
\(\widehat{AHB}=\widehat{ACH}=90^0\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(g.c.g\right)\)
b, Ta có : Ax là tia phân giác của tam giác ABC cắt BC tại H , và cũng là đường cao
=> AH vuông góc với BC
c, Ta có : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{6^2}+\frac{1}{6^2}=\frac{1}{18}\)
\(\Rightarrow AH^2=18\)
\(\Rightarrow AH=\sqrt{18}\)
Thấy câu b sai sai rồi đó bạn @công chúa xinh xắn. Theo mk thì làm thế này nè :v
Ta có :
Góc AHB = AHC ( T/g ABH = T/g ACH )
mà H1 = H2 ( kb ) ( Gọi tắt cho lẹ )
=> H1 = H2 = 180o/2 = 90
=> Ah vuông góc với BC
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H thuộc BC). Chứng minh rằng:
a) H là trung điểm của BC ?
b ) AH là tia phân giác của góc BAC ?
`\color{blue}\text {#DuyNam}`
`a,` Vì Tam giác `ABC` cân `-> AB=AC,`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `ABH` và Tam giác `ACH` có:
\(\widehat{B}=\widehat{C}\)
`AB = AC`
`=>` Tam giác `ABH =` Tam giác `ACH (ch-gn)`
`-> HB=HC (2` cạnh tương ứng `)`
`-> H` là trung điểm của `BC`
`b,` Vì Tam giác `ABH =` Tam giác `ACH (a)`
`->`\(\widehat{BAH}=\widehat{CAH}\) `(2` góc tương ứng `)`
`-> AH` là tia phân giác của \(\widehat{BAC}\)
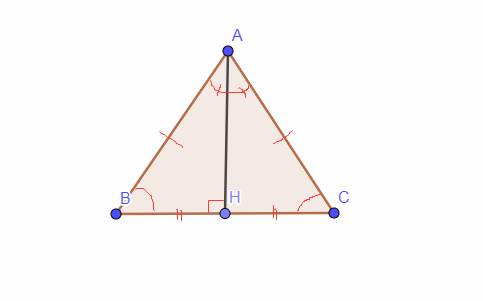
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC (H thuộc BC) a) Chứng minh: Tam giác ABH= tam giác ACH b) Lấy điểm D trên tia đối của tia BC sao cho BD=BH, lấy E trên tia đối của tia BA sao cho BE=BA. Chứng minh: DE//AH
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: Xét tứ giác AHED có
B là trung điểm chung của AE và HD
=>AHED là hình bình hành
=>DE//AH
Cho tam giác ABC cân tại A. Kẻ AH vuông góc BC ( H thuộc BC); kẻ HE vuông góc AB, HF vuông góc AC ( E thuộc AB, F thuộc AC ). Chứng minh:
a) tam giác ABH bằng tam giác ACH
b) AH là tia phân giác của góc A
c) HB = HC
d) tam giác AEH bằng tam giác AFH
giúp mik với mik cảm ơn rất nhiều
A)TRONG TAM GIÁC CÂN ĐƯỜNG CAO CŨNG LÀ DƯỜNG PHÂN GIÁC, PHÁP TUYẾN,TRUNG TUYẾN
=> AH LÀ PHÂN GIÁC CỦA \(\widehat{BAC}\)
XÉT\(\Delta ABC\)CÂN TẠI A
\(\Rightarrow\hept{\begin{cases}AB=AC\\\widehat{B}=\widehat{C}\end{cases}}\)
XÉT \(\Delta ABH\)VÀ\(\Delta ACH\)CÓ
\(\widehat{A_1}=\widehat{A_2}\left(GT\right)\)
\(AB=AC\left(GT\right)\)
\(\widehat{B}=\widehat{C}\left(GT\right)\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(G-C-G\right)\)
B)
TRONG TAM GIÁC CÂN ĐƯỜNG CAO CŨNG LÀ DƯỜNG PHÂN GIÁC, PHÁP TUYẾN,TRUNG TUYẾN
=> AH LÀ PHÂN GIÁC CỦA \(\widehat{BAC}\)
C)VÌ\(\Delta ABH=\Delta ACH\left(CMT\right)\)
=>HB=HC (HAI CẠNH TƯƠNG ỨNG)
D)XÉT\(\Delta AEH\)VÀ\(\Delta AFH\)CÓ
\(\widehat{A_1}=\widehat{A_2}\left(GT\right)\)
D) XÉT TAM GIÁC LÀ ĐƯỢC
Cho tam giác ABC cân tại A, AB > BC, H là trung điểm của BC.
a) Chứng minh: ∆ A B H = ∆ A C H . Từ đó suy ra AH vuông góc với BC.
b) Tính độ dài AH nếu BC = 4 cm, AB = 6 cm.
c) Tia phân giác của góc B cắt AH tại I. Chứng minh tam giác BIC cân.
d) Đường thẳng đi qua A và song song với BC cắt tia BI, CI lần lượt tại M, N. Chứng minh A là trung điểm của đoạn thẳng MN.
e) Kẻ IE vuông góc với AB tại E, IF vuông góc với AC tại F. Chứng minh IH = IE = IF
f) Chứng minh: IC vuông góc với MC.
cho tam giác ABC nhọn và cân tại A, đường cao AH ( H thuộc BC )
a/ chứng minh: \(\Delta\)ABH = \(\Delta\)ACH
b/ chứng minh: tia AH là tia phân giác của BAC
c/ biết AB = 5 cm, BC = 6 cm . tính độ dài của đoạn thẳng BH, AH
a) Vì góc B bằng góc C (tam giác ABC cân tại A)
Và AB =AC
=> tam giác ABH bằng tam giác ACH (cạnh huyền góc nhọn)
b) Trong tam giác ABC cân tại A có AH là đường cao => AH đồng thời là đường phân giác => AH là p/g góc BAC
c) C/m AH là đường trung tuyến như câu b => HB = HC = 3cm
tam giác ABH vuông tại H => \(AH^2+BH^2=AB^2\) => \(AH^2+3^2=5^2\) =>AH = 4cm
đúng nha
a, xét 2 tam giác ABH và ACH vuông tại H ta có:
AB=AC(gt),góc B=góc C từ đó suy ra nha!
b,trong tam giác cân dg cao vừa là dg phân giác trung trực, trung tuyến luôn nên ta suy ra AH là ............(đcpcm)
c, ta có BH=HC=BC/2=6/2=3
áp dụng đ/lí py-ta-go cho tam giác vuông ABH ta có
AB^2=AH^2+BH^2
suy ra: AH^2=AB^2-BH^2
=5^2- 3^2= 25-9 đến đây dễ lắm lun rồi đó bạn!!