bài tập : tìm x
a: 2 [x+5] - x2 - 5x =0
b: 2 [x-3] [x2 +1] + 15x - 5x2 =0
c: [x+2] [3-4x] = x2 + 4x +4
giúp với mọi người ơi còn 1 bài mà tôi mãi không nghĩ ra
Bài 2: Tìm x, biết:
a)5(x + 3)-2(3 + x) = 0
b)6x(x2 - 2) - (2 - x2) = 0
c)4x(x - 2013) - x + 2013 = 0
d)(x + 1)2 = x + 1
\(a,\Leftrightarrow3\left(x+3\right)=0\Leftrightarrow x=-3\\ b,\Leftrightarrow\left(x^2-2\right)\left(6x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2=2\\6x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{2}\\x=-\sqrt{2}\\x=-\dfrac{1}{6}\end{matrix}\right.\\ c,\Leftrightarrow\left(x-2013\right)\left(4x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2013\\x=\dfrac{1}{4}\end{matrix}\right.\\ d,\Leftrightarrow\left(x+1\right)^2-\left(x+1\right)=0\\ \Leftrightarrow\left(x+1\right)\left(x+1-1\right)=0\\ \Leftrightarrow x\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
Giải phương trình bằng cách đặt ẩn phụ:
a ) 3. x 2 + x 2 − 2 x 2 + x − 1 = 0 b ) x 2 − 4 x + 2 2 + x 2 − 4 x − 4 = 0 c ) x − x = 5 x + 7 d ) x x + 1 − 10 ⋅ x + 1 x = 3
a)
3 · x 2 + x 2 - 2 x 2 + x - 1 = 0 ( 1 )
Đặt t = x 2 + x ,
Khi đó (1) trở thành : 3 t 2 – 2 t – 1 = 0 ( 2 )
Giải (2) : Có a = 3 ; b = -2 ; c = -1
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 ; t 2 = c / a = - 1 / 3 .
+ Với t = 1 ⇒ x 2 + x = 1 ⇔ x 2 + x – 1 = 0 ( * )
Có a = 1; b = 1; c = -1 ⇒ Δ = 1 2 – 4 . 1 . ( - 1 ) = 5 > 0
(*) có hai nghiệm
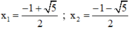
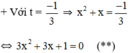
Có a = 3; b = 3; c = 1 ⇒ Δ = 3 2 – 4 . 3 . 1 = - 3 < 0
⇒ (**) vô nghiệm.
Vậy phương trình (1) có tập nghiệm 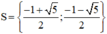
b)
x 2 − 4 x + 2 2 + x 2 − 4 x − 4 = 0 ⇔ x 2 − 4 x + 2 2 + x 2 − 4 x + 2 − 6 = 0 ( 1 )
Đặt x 2 – 4 x + 2 = t ,
Khi đó (1) trở thành: t 2 + t – 6 = 0 ( 2 )
Giải (2): Có a = 1; b = 1; c = -6
⇒ Δ = 1 2 – 4 . 1 . ( - 6 ) = 25 > 0
⇒ (2) có hai nghiệm
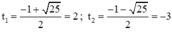
+ Với t = 2 ⇒ x 2 – 4 x + 2 = 2
⇔ x 2 – 4 x = 0
⇔ x(x – 4) = 0
⇔ x = 0 hoặc x = 4.
+ Với t = -3 ⇒ x 2 – 4 x + 2 = - 3
⇔ x2 – 4x + 5 = 0 (*)
Có a = 1; b = -4; c = 5 ⇒ Δ ’ = ( - 2 ) 2 – 1 . 5 = - 1 < 0
⇒ (*) vô nghiệm.
Vậy phương trình ban đầu có tập nghiệm S = {0; 4}.
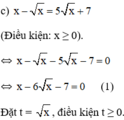
Khi đó (1) trở thành: t 2 – 6 t – 7 = 0 ( 2 )
Giải (2): Có a = 1; b = -6; c = -7
⇒ a – b + c = 0
⇒ (2) có nghiệm t 1 = - 1 ; t 2 = - c / a = 7 .
Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.
+ Với t = 7 ⇒ √x = 7 ⇔ x = 49 (thỏa mãn).
Vậy phương trình đã cho có nghiệm x = 49.
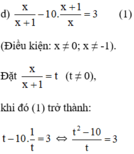
⇔ t 2 – 10 = 3 t ⇔ t 2 – 3 t – 10 = 0 ( 2 )
Giải (2): Có a = 1; b = -3; c = -10
⇒ Δ = ( - 3 ) 2 - 4 . 1 . ( - 10 ) = 49 > 0
⇒ (2) có hai nghiệm:
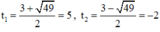
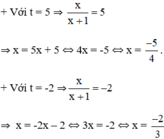
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình đã cho có tập nghiệm 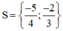
phân tích đa thức thành nhân tử . Câu hỏi của nguoiemtinhthong.
Bài 1.1.2x2+5x−1=7x3−1−−−−−√1.1.2x2+5x−1=7x3−1
Bài 1.2.3x−1−−−−√+2x+1−−−−√=5x2−1−−−−−√41.2.3x−1+2x+1=5x2−14
Bài 1.3.3x2+4x−5−−−−−−−−−√+x−3−−−−√=11x2+25x+2−−−−−−−−−−−−√1.3.3x2+4x−5+x−3=11x2+25x+2
Bài 1.4.2x2−2x+2=3(x−2)(x2+x)−−−−−−−−−−−−√1.4.2x2−2x+2=3(x−2)(x2+x)
Bài 1.5.4x2−4x−10=8x2−6x−10−−−−−−−−−−−√1.5.4x2−4x−10=8x2−6x−10
Bài 1.6.2x2+3x+1−−−−−−−−−−√−2x2−2−−−−−−√=x+1
Nếu ol thì tham khảo nah nguoiemtinhthong.
1.1
2x2+5x−1=7x3−1−−−−−√2x2+5x−1=7x3−1
⇔2(x2+x+1)+3(x−1)−7(x−1)(x2+x+1)−−−−−−−−−−−−−−−√(1)⇔2(x2+x+1)+3(x−1)−7(x−1)(x2+x+1)(1)
Đặt a=x−1−−−−−√;b=x2+x+1−−−−−−−−√;a≥0;b>0a=x−1;b=x2+x+1;a≥0;b>0
pt (1) trở thành 3a2+2b2−7ab=03a2+2b2−7ab=0
a=2ba=2b v a=13ba=13b
Các bạn tự giải quyết tiếp nhé.
1.2
TXĐ D=[1;+∞)D=[1;+∞)
đặt a=x−1−−−−−√4;b=x+1−−−−−√4;a,b≥0a=x−14;b=x+14;a,b≥0
pt (2) trở thành 3a2+2b2−5ab=03a2+2b2−5ab=0
⇔a=b⇔a=b v a=23ba=23b
...
1.3
D=[3;+∞)D=[3;+∞)
Đặt a=x2+4x−5−−−−−−−−−√;b=x−3−−−−−√;a,b≥0a=x2+4x−5;b=x−3;a,b≥0
pt (3) trở thành 3a+b=11a2−19b2−−−−−−−−−√3a+b=11a2−19b2
⇔2a2−6ab−20b2=0⇔2a2−6ab−20b2=0
⇒a=5b⇒a=5b
...
1.4
ĐK
⇔2x2−2x+2=3(x−2)x(x+1)−−−−−−−−−−−−√2x2−2x+2=3(x−2)x(x+1)
⇔(x2−2x)+2(x+1)=3(x2−2x)(x+1)−−−−−−−−−−−−−√2(x2−2x)+2(x+1)=3(x2−2x)(x+1)
Đặt x2−2x−−−−−−√=ax2−2x=a; x+1−−−−−√=bx+1=b (a;b\geq0)
⇔2a2+2b2=3ab
1.5
Đặt 4x2−4x−10=t4x2−4x−10=t (t \geq 0)
⇔t=t+4x2−2x−−−−−−−−−−√t=t+4x2−2x
⇔t2−t−4x2+2x=0t2−t−4x2+2x=0
Δ=1−4(2x−4x2)=(4x−1)2Δ=1−4(2x−4x2)=(4x−1)2
⇒t=1−2xt=1−2x hoặc t=2xt=2x
1.1
2.2+5.-1=7.3-1-----v2.2+5.-1=7.3-1
2(.2+x+1)+3(x-1)
3a+b=11a2-19b2
tóm tắt
bài 1 giải các bất phương trình sau
a, -x2 +5x-6 ≥ 0
b, x2-12x +36≤0
c, -2x2 +4x-2≤0
d, x2 -2|x-3| +3x ≥ 0
e, x-|x+3| -10 ≤0
bài 2 xét dấu các biểu thức sau
a,<-x2+x-1> <6x2 -5x+1>
b, x2-x-2/ -x2+3x+4
c, x2-5x +2
d, x-< x2-x+6 /-x2 +3x+4 >
Bài 1:
a: \(\Leftrightarrow x^2-5x+6< =0\)
=>(x-2)(x-3)<=0
=>2<=x<=3
b: \(\Leftrightarrow\left(x-6\right)^2< =0\)
=>x=6
c: \(\Leftrightarrow x^2-2x+1>=0\)
\(\Leftrightarrow\left(x-1\right)^2>=0\)
hay \(x\in R\)
Giải các phương trình sau:
a/ (3x – 2)(4x + 5) = 0
b/ (2,3x – 6,9)(0,1x + 2) = 0
c/ (4x + 2)(x2 + 1) = 0
d/(2x + 7)(x – 5)(5x + 1) = 0
e/ (x – 1)(2x + 7)(x2 + 2) = 0
f/ (3x + 2)(x2 – 1) = (9x2 – 4)(x + 1)
a) \(\left(3x-2\right)\left(4x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-2=0\\4x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{5}{4}\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{2}{3};-\dfrac{5}{4}\right\}\)
b) \(\left(2,3x-6,9\right)\left(0,1x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2,3x-6,9=0\\0,1x+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-20\end{matrix}\right.\)
c) \(\left(4x+2\right)\left(x^2+1\right)=0\)
Vì \(x^2+1\ge1>0\forall x\)
\(\Rightarrow4x+2=0\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy: \(S=\left\{-\dfrac{1}{2}\right\}\)
d) \(\left(2x+7\right)\left(x-5\right)\left(5x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+7=0\\x-5=0\\5x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{7}{2}\\x=5\\x=-\dfrac{1}{5}\end{matrix}\right.\)
Vậy: \(S=\left\{-\dfrac{7}{2};5;-\dfrac{1}{5}\right\}\)
e) \(\left(x-1\right)\left(2x+7\right)\left(x^2+2\right)=0\)
Vì \(x^2+2\ge2>0\forall x\)
\(\Rightarrow\left(x-1\right)\left(2x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+7=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{7}{2}\end{matrix}\right.\)
f) \(\left(3x+2\right)\left(x^2-1\right)=\left(9x^2-4\right)\left(x+1\right)\)
\(\Leftrightarrow\left(3x+2\right)\left(x-1\right)\left(x+1\right)-\left(3x-2\right)\left(3x+2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[\left(3x+2\right)\left(x+1\right)\right].\left(x-1-3x+2\right)=0\)
\(\Leftrightarrow\left(3x^2+5x+2\right)\left(-2x+1\right)=0\)
\(\Leftrightarrow\left(3x^2+3x+2x+2\right)\left(-2x+1\right)=0\)
\(\Leftrightarrow\left[3x\left(x+1\right)+2\left(x+1\right)\right]\left(-2x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x+2\right)\left(-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\3x+2=0\\-2x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{2}{3}\\x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy: \(S=\left\{-1;-\dfrac{2}{3};\dfrac{1}{2}\right\}\)
Bài 1: Làm tính nhân
a. 3x2 (5x2 - 4x +3)
b. – 5xy(3x2y – 5xy +y2 )
c. (5x2 - 4x)(x -3)
d. (x – 3y)(3x2 + y2 +5xy)
Bài 2: Rút gọn các biểu thức sau.
a.(x-3)(x + 7) – (x +5)(x -1)
b. (x + 8)2 – 2(x +8)(x -2) + (x -2)2
c. x2 (x – 4)(x + 4) – (x2 + 1)(x2 - 1)
d. (x+1)(x2 – x + 1) – (x – 1)(x2 +x +1)
Bài 1:
\(a,=15x^4-12x^3+9x^2\\ b,=-15x^3y^2+25x^2y^2-5xy^3\\ c,=5x^3-15x^2-4x^2+12x=5x^3-19x^2+12x\\ d,=3x^3-9x^2y+xy^2-3y^3+5x^2y-15xy^2=3x^3-3y^3-4x^2y-14xy^2\)
Bài 2:
\(a,=x^2+4x-21-x^2-4x+5=-16\\ b,=x^2+16x+64-2x^2-12x+32+x^2-4x+4=100\\ c,=x^4-16x^2-x^4+1=1-16x^2\\ d,=x^3+1-x^3+1=2\)
Bài 1: Làm tính nhân:
a. 3x2(5x2- 4x +3) b. – 5xy(3x2y – 5xy +y2)
c. (5x2- 4x)(x -3) d. (x – 3y)(3x2 + y2 +5xy)
Bài 2: Rút gọn các biểu thức sau:
a.(x-3)(x + 7) – (x +5)(x -1) b. (x + 8)2 – 2(x +8)(x -2) + (x -2)2
c. x2(x – 4)(x + 4) – (x2 + 1)(x2- 1) d. (x+1)(x2 – x + 1) – (x – 1)(x2 +x +1)
Bài 3: Phân tích các đa thức sau thành nhân tử:
a. – 24x^2y^2 + 12xy^3
b. x2 – 6 x +xy - 6y
c. 2x2 + 2xy - x - y
d. ax – 2x - a2 +2a
e. x3- 3x2 + 3x -1
f. 3x2 - 3y2 - 12x – 12y
g. x2 - 2xy – x2 + 4y2
h. x2 + 2x + 1 - 16
i. x2 - 4x + 4 - 25y2
k. x2 - 6xy + 9y2 -25z2
l. 81 – x2 + 4xy – 4y2
m.x2 +6x –y2 +9
n.x2 – 2x - 4y2 + 1
o. x2 – 2x -3
p. x2 + 4x -12 q. x2 + x – 6
s. x2 -5x -6
t. x2 - 8 x – 9
u, x2 + 3x – 18
v, x2 - 8x +15
x, x2 + 6x +8
z, x2 -7 x + 6
w, 3x2 - 7x + 2
y, x4 + 64
Bài 4: Tìm x biết:
a. x2-25 –( x+5 ) = 0
b. 3x(x-2) – x+ 2 = 0
c. x( x – 4) - 2x + 8 = 0
d. 3x (x + 5) – 3x – 15=0
e. ( 3x – 1)2 – ( x +5)2=0
f. ( 2x -1)2 – ( x -3)2=0
g.(2x -1)2- (4x2 – 1) = 0
g. x2(x2 + 4) – x2 – 4 = 0
i.x4 - x3 +x2 - x =0
k. 4x2 – 25 –( 2x -5)(2x +7)=0
l.x3 – 8 – (x -2)(x -12) = 0
m.2(x +3) –x2– 3x=0
Bài 5: Làm phép chia:
a. (x4+ 2x3+ 10x – 25) : (x2 + 5) b. (x3- 3x2+ 5x – 6): ( x – 2)
Bài 6: Tìm số a để đa thức 3x3 + 2x2 – 7x + a chia hết cho đa thức 3x – 1
Tìm x biết:
a) (x+5).(2x+1)=0
b) x.(x+2)-3.(x+2)=0
c) 2x.(x-5)-x.(3+2x)=26
d) x2-10x-8x+16=0
e) x2-10x=25
f) 5x.(x-1)=x-1
g) 2.(x+5)-x2-5x=0
h) x2+5x-6=0
i) (2x-3)2-4.(x+1).(x-1)=49
j) x3+x2+x+1=0
k) x3-x2=4x2-8x+4
Mn ơi giúp em vs ạ,em cảm ơn trc ạ
\(a,\Leftrightarrow\left[{}\begin{matrix}x+5=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-\dfrac{1}{2}\end{matrix}\right.\\ b,\Leftrightarrow\left(x+2\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\\ c,\Leftrightarrow2x^2-10x-3x-2x^2=26\\ \Leftrightarrow-13x=26\Leftrightarrow x=-2\\ d,\Leftrightarrow x^2-18x+16=0\\ \Leftrightarrow\left(x^2-18x+81\right)-65=0\\ \Leftrightarrow\left(x-9\right)^2-65=0\\ \Leftrightarrow\left(x-9+\sqrt{65}\right)\left(x-9-\sqrt{65}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=9-\sqrt{65}\\9+\sqrt{65}\end{matrix}\right.\)
\(e,\Leftrightarrow x^2-10x-25=0\\ \Leftrightarrow\left(x-5\right)^2-50=0\\ \Leftrightarrow\left(x-5-5\sqrt{2}\right)\left(x-5+5\sqrt{2}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=5+5\sqrt{2}\\x=5-5\sqrt{2}\end{matrix}\right.\\ f,\Leftrightarrow5x\left(x-1\right)-\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(5x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{5}\end{matrix}\right.\\ g,\Leftrightarrow2\left(x+5\right)-x\left(x+5\right)=0\\ \Leftrightarrow\left(2-x\right)\left(x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\\ h,\Leftrightarrow x^2+2x+3x+6=0\\ \Leftrightarrow\left(x+3\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-2\end{matrix}\right.\\ i,\Leftrightarrow4x^2-12x+9-4x^2+4=49\\ \Leftrightarrow-12x=36\Leftrightarrow x=-3\)
\(j,\Leftrightarrow x^2\left(x+1\right)+\left(x+1\right)=0\Leftrightarrow\left(x^2+1\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2=-1\left(vô.lí\right)\\x=-1\end{matrix}\right.\Leftrightarrow x=-1\\ k,\Leftrightarrow x^2\left(x-1\right)=4\left(x-1\right)^2\\ \Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Bài 1: Rút gọn
C) (x2 - 3) (x2 +3) - 5x2 (x + 1)2 - (x2 - 3x) ( x2 - 2x) + 4x (x + 2)2
D) -6x2 (x + 5)2 - ( x - 3)2 + (x2 - 2) (2x2 + 1) - 4x2 ( 3x - 4)2
A) -2x(3x+2)(3x-2)+5(x+2)2 - (x-1)(2x+1)(2x+1)
= -2x(9x2-4)+5(x2+4x+4) - (x-1)(4x2-1)
= -18x3+8x+5x2+20x+20-(4x3-x-4x2+1)
= -18x3+5x2+28x+20-4x3+x+4x2+1
= -22x3+9x2+29x+21
B) (7x-8)(7x+8)-10(2x+3)2+5x(3x-2)2-4x(x-5)2
= 49x2 - 64 -10(4x2+ 12x + 3) + 5x(9x2 - 12x +4) - 4x(x2 - 10x +25)
= 49x2 - 64 -40x2 - 120x - 30 + 45x3 - 60x2 - 20x - 4x3 + 40x2 -100x
= 41x3 -11x2 -240x -94
C) \(\left(x^2-3\right)\left(x^2+3\right)-5x^2\left(x+1\right)^2-\left(x^2-3x\right)\left(x^2-2x\right)+4x\left(x+2\right)^2\)
\(\left(x^4-9\right)-5x^2\left(x^2+2x+1\right)-\left(x^4-2x^3-3x^3+6x^2\right)+4x\left(x^2+4x+4\right)\)
\(x^4-9-5x^4-10x^3-5x^2-x^4+5x^3-6x^2+4x^3+16x^2+16x\)
\(-5x^4-x^3+5x^2+20x-9\)
D) \(-6x^2\left(x+5\right)^2-\left(x-3\right)^2+\left(x^2-2\right)\left(2x^2+1\right)-4x^2\left(3x-4\right)^2\)
\(-6x^2\left(x^2+10x+25\right)-\left(x^2-6x+9\right)+2x^4-3x^2-2-4x^2\left(9x^2-24x+16\right)\)
\(-6x^4-60x^3+150x^2-x^2+6x-9+2x^4-3x^2-2-36x^4+96x^3-64x^2\)
\(-40x^4+36x^3+82x^2+6x-11\)