Tính khoảng cách giữa 2 đường thẳng sau
(Δ1) : x+2y-10 = 0 và (Δ2): 4x+2y-1 = 0
Những câu hỏi liên quan
Tính góc giữa hai đường thẳng ∆1 và ∆2 trong trường hợp sau: Δ1: 2x + y – 4 = 0 và Δ2 : 5x – 2y + 3 = 0.
Hai đường thẳng Δ1 và Δ2 có vecto pháp tuyến lần lượt là: n1→(2;1); n2→(5;-2)
Góc giữa hai đường thẳng (Δ1) và (Δ2) là:
Đúng 1
Bình luận (0)
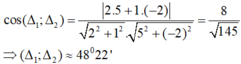
Côsin góc giữa 2 đường thẳng Δ1: x + 2y - 2 = 0 và Δ2: x - y = 0 là:
A. 10 10
B. 2
C. 2 3
D. 3 3
Góc giữa hai đường thẳng Δ1: 5x - y + 2 = 0 và Δ2: 3x + 2y + 1 = 0 là:
A. 30 °
B. 90 °
C. 45 °
D. 0 °
Chọn C.
Ta có:
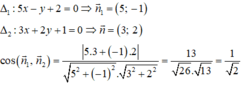
Vậy góc giữa hai đường thẳng Δ1, Δ2 là 45 ° .
Đúng 0
Bình luận (0)
Trên mặt phẳng Oxy, hình chữ nhật ABCD có đỉnh A(3;- 1) và Δ1:x−2y+10, Δ2:2x+y0 là hai trong bốn đường thẳng chứa bốn cạnh của hình chữ nhật đó. Diện tích của ABCD bằng
Đọc tiếp
Trên mặt phẳng Oxy, hình chữ nhật ABCD có đỉnh A(3;- 1) và là hai trong bốn đường thẳng chứa bốn cạnh của hình chữ nhật đó. Diện tích của ABCD bằng
Thay tọa độ A vào 2 pt đường thẳng không thỏa mãn, vậy đó là 2 pt đường thẳng của các cạnh BC và CD
\(\Rightarrow\) Khoảng cách từ A đến 2 đường thẳng nói trên bằng độ dài 2 cạnh của hcn
\(\Rightarrow S=d\left(A;\Delta_1\right).d\left(A;\Delta_2\right)=\dfrac{\left|3-2.\left(-1\right)+1\right|}{\sqrt{1^2+\left(-2\right)^2}}.\dfrac{\left|2.3-1\right|}{\sqrt{2^2+1^2}}=6\)
Đúng 2
Bình luận (0)
Cho hàm số
y
2
x
x
-
2
có đồ thị (C). Tìm giá trị nhỏ nhất h của tổng khoảng cách từ điểm M thuộc (C) tới hai đường thẳng
Δ
1
:
x
-
1
0
;
Δ
2
:
y
-
2
0
. A. h 4 B...
Đọc tiếp
Cho hàm số y = 2 x x - 2 có đồ thị (C). Tìm giá trị nhỏ nhất h của tổng khoảng cách từ điểm M thuộc (C) tới hai đường thẳng Δ 1 : x - 1 = 0 ; Δ 2 : y - 2 = 0 .
A. h = 4
B. h = 3
C. h = 5
D. h = 2
Cosin của góc giữa hai đường thẳng Δ1: a1x + b1y + c1 0 và Δ2: a2x + b2y + c2 0 là: A.
cos
(
∆
1
;
∆
2
)
a
1
b
1
+
a
2
b...
Đọc tiếp
Cosin của góc giữa hai đường thẳng Δ1: a1x + b1y + c1 = 0 và Δ2: a2x + b2y + c2 = 0 là:
A. cos ( ∆ 1 ; ∆ 2 ) = a 1 b 1 + a 2 b 2 a 1 2 + b 1 2 . a 2 2 + b 2 2
B. cos ( ∆ 1 ; ∆ 2 ) = a 1 a 2 + b 1 b 2 a 1 2 + a 2 2 . b 1 2 + b 2 2
C. cos ( ∆ 1 ; ∆ 2 ) = a 1 a 2 + b 1 b 2 a 1 2 + b 1 2 . a 2 2 + b 2 2
D. cos ( ∆ 1 ; ∆ 2 ) = a 1 a 2 + b 1 b 2 a 1 2 + b 1 2 . a 2 2 + b 2 2
Tính góc giữa hai đường thẳng ∆1 và ∆2 trong các trường hợp sau: Δ1: y = –2x + 4 và Δ2: y = x 2 + 3 2
Cách 1:
Δ1: y = –2x + 4 ⇔ 2x + y – 4 = 0
Δ2: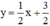 
⇔ x - 2y + 3 = 0
Hai đường thẳng Δ1 và Δ2 có vecto pháp tuyến lần lượt là: n1→(2;1); n2→(1;-2)
Góc giữa (Δ1) và (Δ2):
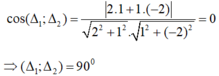
Cách 2:
Δ1: y = –2x + 4 có hệ số góc k1 = –2
Δ2: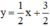 
có hệ số góc k2 = 1/2
Nhận thấy k1.k2 = –1 nên Δ1 ⊥ Δ2 ⇒ (Δ1, Δ2) = 90°.
Đúng 0
Bình luận (0)
Tìm tập hợp các điểm cách đều hai đường thẳng: (Δ1): 5x + 3y – 3 = 0 và (Δ2) : 5x + 3y + 7 = 0.
Gọi điểm cách đều hai đường thẳng (Δ1) và (Δ2) là M(x, y).
Ta có:
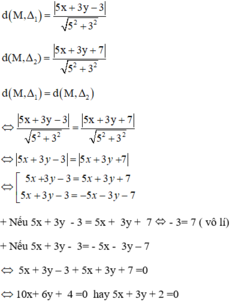
Vậy tập hợp các điểm M cách đều hai đường thẳng đã cho là đường thẳng: 5x + 3y + 2 = 0.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai đường thẳng
Δ
1
:
x
-
4
3
y
-
1
-
2
z
+
5
-
1
và
Δ
2...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng Δ 1 : x - 4 3 = y - 1 - 2 = z + 5 - 1 và Δ 2 : x - 2 1 = y + 3 3 = z 1 . Giả sử M ∈ Δ 1 , N ∈ Δ 2 sao cho MN là đoạn vuông góc chung của hai đường thẳng ∆ 1 và ∆ 2 . Tính M N →
A. M N → 5 ; - 5 ; 10
B. M N → 2 ; - 2 ; 4
C. M N → 3 ; - 3 ; 6
D. M N → 1 ; - 1 ; 2
